

分析 (1)先证明△ABP∽△PCD,再根据相似比得出CD的长;
(2)延长线段AP、DC交于点E,根据ASA证明△DPA≌△DPE,得PA=PE,再根据AAS证明△APB≌△EPC,得PB=PC;
(3)先做出图形,再根据△PDC是等腰三角形,得△PAB是等腰三角形,求得PC,根据点B与点B′关于AP 对称,得四边形ABPB′是正方形,四边形B′PCE是矩形,再得出DE的长,在Rt△B′DE中,由勾股定理,得B′D.
解答  解:(1)∵AB⊥BC,CM⊥BC,DP⊥AP,
解:(1)∵AB⊥BC,CM⊥BC,DP⊥AP,
∴∠ABP=∠APD=∠PCD=90°,
∴∠APB=∠PDC,
∴△ABP∽△PCD,
∴$\frac{AB}{PC}$=$\frac{PB}{CD}$,
∵BC=5,AB=1,BP=4,
∴CP=1
∴CD=4.
(2)PB=PC,
理由如下:延长线段AP、DC交于点E
∵DP平分∠ADC,
∴∠ADP=∠EDP.
∵DP⊥AP,
∴∠DPA=∠DPE=Rt∠.
在△DPA和△DPE中,$\left\{\begin{array}{l}{∠ADP=∠EDP}\\{DP=DP}\\{∠DPA=∠DPE}\end{array}\right.$,
∴△DPA≌△DPE(ASA),
∴PA=PE.
∵AB⊥BP,CM⊥CP,∴∠ABP=∠ECP=Rt∠.
在△APB和△EPC中,$\left\{\begin{array}{l}{∠ABP=∠ECP}\\{∠APB=∠EPC}\\{PA=PE}\end{array}\right.$,
∴△APB≌△EPC(AAS),
∴PB=PC;
(3)∵△PDC是等腰三角形,∠C=90°,
∴PC=CD,∠DPC=∠PDC=45°.
∵DP⊥AP,
∴∠APD=90°,
∵∠APB+∠DPC=90°.
∴∠APB=45°
∵AB⊥BC,
∴∠B=90°,
∴∠BAP+∠APB=90°,
∴∠BAP=45°,
∴∠BAP=∠BPA,
∴AB=PB=1.
∴PC=3
∵点B与点B′关于AP 对称,
∴△ABP≌AB′P,
∴BP=PB′=1.AB=AB′.
∵∠B=90°,
∴四边形ABPB′是正方形,
∴∠BPB′=90°,
∴∠B′PC=90°,
∵B′E⊥CD,
∴∠B′EC=90°.
∴四边形B′PCE是矩形,
∴PB′=CE=1,B′E=PC=3,
∴DE=2,
在Rt△B′DE中,由勾股定理,得B′D=$\sqrt{13}$.
故答案为$\sqrt{13}$.
点评 本题考查了几何变换综合题,以动点问题为背景,主要考查了等腰直角三角形的性质,勾股定理,全等三角形的判定与性质,以及矩形的性质的综合应用,解决问题的关键是作辅助线构造全等三角形,以及灵活运用勾股定理计算线段的长度.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
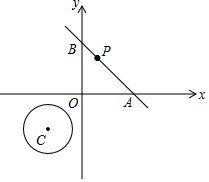 如图,在平面直角坐标系中,O为坐标原点,⊙C的圆心坐标为(-2,-2),半径为$\sqrt{2}$.函数y=-x+2图象与x轴交于点A,与y轴交于点B,点P为线段AB上一动点(包括端点).
如图,在平面直角坐标系中,O为坐标原点,⊙C的圆心坐标为(-2,-2),半径为$\sqrt{2}$.函数y=-x+2图象与x轴交于点A,与y轴交于点B,点P为线段AB上一动点(包括端点).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
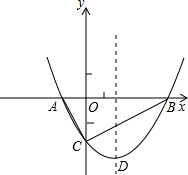 如图,抛物线y=x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
如图,抛物线y=x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
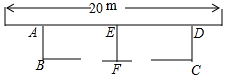 如图,利用一面墙(墙的长度为20m),用34m长的篱笆围成两个鸡场,中间用一道篱笆隔开,每个鸡场均留一道1m宽的门,设AB的长为x米.
如图,利用一面墙(墙的长度为20m),用34m长的篱笆围成两个鸡场,中间用一道篱笆隔开,每个鸡场均留一道1m宽的门,设AB的长为x米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com