
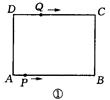
如图①,在矩形 ABCD中,AB=10cm,BC=8cm.点P从A出发,沿A→B→C→D路线运动,到D停止;点Q从D出发,沿 D→C→B→A路线运动,到A停止.若点P、点Q同时出发,点P的速度为每秒1cm,点Q的速度为每秒2cm,a秒时点P、点Q同时改变速度,点P的速度变为每秒bcm,点Q的速度变为每秒dcm.图②是点P出发x秒后△APD的面积S1(cm2)与x(秒)的函数关系图象;图③是点Q出发x秒后△AQD的面积S2(cm2)与x(秒)的函数关系图象.
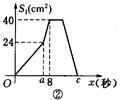
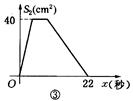
(1)参照图象,求b、图②中c及d的值;
(2)连接PQ,当PQ平分矩形ABCD的面积时,运动时间x的值为 ;
(3)当两点改变速度后,设点P、Q在运动线路上相距的路程为y(cm),求y(cm)与运动时间x(秒)之间的函数关系式,并写出自变量x的取值范围;
(4)若点P、点Q在运动路线上相距的路程为25cm,求x的值.
(1)b=2(厘米/秒),c=17(秒),d=1(厘米/秒);(2)或;
(3)当6<x≤时,y=―3x+28;当<x≤17时,y=3x―28;
当17<x≤22时,y=x+6;
(4)1或19.
【解析】试题分析:(1)观察图1和2,得
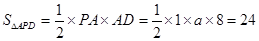 (平方厘米)
(平方厘米)
∴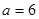 (秒)
(秒)
b= (厘米/秒)
(厘米/秒)
c=8+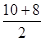 =17(秒)
=17(秒)
依题意得(22-6)d=28-12
解得d=1(厘米/秒);
(2)由题意可得,
当0<x≤5时,假设(x+2x)×8×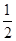 =〔(10-2x)+(10-x)〕×8×
=〔(10-2x)+(10-x)〕×8×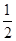
则x=(符合题意)
当5<x≤13时,由图可知,没有符合的解
当13<x≤22时, +13=(符合题意);
(3)当6<x≤时,y=―3x+28;
当<x≤17时,y=3x―28;
当17<x≤22时,y=x+6;
(4)当点Q出发17秒时,点P到达点D停止运动,点Q还需运动2秒,
即共运动19秒时,可使P、Q这两点在运动路线上相距的路程为25cm.
点Q出发1s,则点P,Q相距25cm,设点Q出发x秒,点P、点Q相距25cm,
则2x+x=28-25,
解得x=1.
∴当点Q出发1或19秒时,点P、点Q在运动路线上相距的路程为25cm.
本题涉及了直角坐标系的意义和动点构成的几何意义,该题在分析上较为复杂,要求学生在原来图形中找出不变的元素,结合直角坐标系所表示的几何意义加以分析,找出规律。


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源:名师精选(解析版)8 题型:解答题
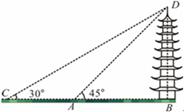
如图,西园中学数学兴趣小组的同学欲测量一座垂直于地面的古塔BD的高度,他们先在A处测得古塔顶端点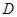 的仰角为
的仰角为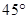 ,再沿着
,再沿着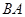 的方向后退20m至
的方向后退20m至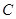 处,测得古塔顶端点
处,测得古塔顶端点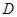 的仰角为
的仰角为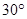 ,求该古塔BD的高度(
,求该古塔BD的高度(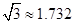 ,结果保留一位小数).
,结果保留一位小数).
查看答案和解析>>
科目:初中数学 来源:名师精选(解析版)8 题型:解答题
初三年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:

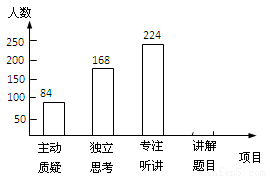
(1)在这次评价中,一共抽查了 名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为 度;
(3)请将频数分布直方图补充完整;
(4)如果全市有6000名初三学生,那么在试卷评讲课中,“独立思考”的初三学生约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com