
����Ŀ��һ��С�ͷ�ӳ��ӯ����y��Ԫ������Ʊ��x���ţ�֮��Ĺ�ϵ��ͼ�����ղ��Ź涨�����ڳ���150�ˣ�Ҫ���ɱ��շ�50Ԫ���Ը���ͼ��ش����⣺

��1���÷�ӳ���� ����λ���÷�ӳ���ݳ�һ����Ӱ�������ɱ��ܺ��� Ԫ��ÿ��Ʊ���ۼ��� Ԫ��
��2������Ʊ��xΪ ʱ�����ⲻ����Ʊ��xΪ ʱ���Ȿ��Ҫ����������150Ԫ����Ʊ��xӦΪ ��.
��3������Ʊ��x�Ƕ�����ʱ�����õ����������150��ʱ��������ȣ��з��̽�𣩣�����Ʊ������ʲô����ʱ����ʱ�����x��150��ʱ�ࣿ
���𰸡���1��200����200Ԫ��2Ԫ/��.��2��100�ţ�0��x<100��x=184.��3��x=125�����۳���Ʊ������167С�ڵ���200ʱ,����õ������x=150ʱ��..
��������
��1���۲�ͼ���֪�÷�ӳ���ж��ٸ���λ�ͷ�ӳ���ݳ�һ����Ӱ�������ɱ��ܺͣ�ͬʱ����ͼ���֪��100������Ϊ0���ٸ��ݳɱ���֪��ÿ��Ʊ��.��2����ʱ0��x��150ʱ,һ�κ���ͼ����x���ཻ,���ݽ�������,�����ⲻ,�Ȿ,���������xȡֵ��Χ;��150<x��200ʱ,����һ�κ���ͼ���֪����������150Ԫ�۶�����Ʊ.��3����������150��ʱ������Ϊ50Ԫ��Ȼ���y=50����y=2x-200���x���ɣ�x=150ʱ,y=100,��y=100����150<x��200�ĺ���ʽ,��x��ֵ,��������ȶ�ʱ,x��ȡֵ��Χ.
��1���۲�ͼ���֪�÷�ӳ����200����λ�ͷ�ӳ���ݳ�һ����Ӱ�������ɱ��ܺ�200Ԫ������Ϊ��100������Ϊ0������ÿ��Ʊ���ۼ�=200��100=2Ԫ/��.
��2����ʱ0��x��150ʱ,���߶ν���ʽΪy=ax+b���ѣ�0��-200������150��100�������b=-200��150a+b=100.���a=2��b=-200�����Ժ�������ʽΪy=2x-200����x=0��x=100�����Ե��۳�100��Ʊʱ����ʱ�����⣻��0��x<100ʱ����ʱ�Ȿ����150<x��200ʱ,���߶ν���ʽΪy=mx+n���ѣ�150��50����200��200�������150m+n=50��200m+n=200���m=3��n=-400�����Ժ�������ʽΪy=3x-400����y=150ʱ�������x=![]() ,��ΪxΪ��������Ϊ184��.
,��ΪxΪ��������Ϊ184��.
��3����������ã�������150��ʱ������Ϊ50Ԫ�����Ե�y=50ʱ����y=2x-200��x=125�����Ե�x=125ʱ�����õ����������150��ʱ��������ȣ���y=100����y=3x-400�е�100=3x-400�����x=![]() ����ΪxΪ���������Ե��۳���Ʊ������167С�ڵ���200ʱ,����õ������x=150ʱ��.
����ΪxΪ���������Ե��۳���Ʊ������167С�ڵ���200ʱ,����õ������x=150ʱ��.


 �ƸԺ���ȫ�����Ų��Ծ�ϵ�д�
�ƸԺ���ȫ�����Ų��Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
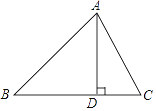
����Ŀ������ABC�У�AB=15��BC=14��AC=13������ABC�������
ijѧϰС�龭����������������������Ľ���˼·��
��AD��BC��D����BD=x���ú�x�Ĵ���ʽ��ʾCD�����ݹ��ɶ���������AD��Ϊ�����������г��������x�������AD�ij����Ӷ����������ε���������㰴�����ǵĽ���˼·��ɽ����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�ƻ������ס������ֹ�������鷢�֣�������������3�����������2���������ʽ�1020Ԫ��������������4�����������3���������ʽ�1440Ԫ��
��1���ס����������ÿ���ļ۸�ֱ��Ƕ���Ԫ?
��2������У�ƻ����������ֹ������20�������������������������ڼ�������������ѧУ�����ܹ��ṩ�ʽ�4320Ԫ������Ƽ��ֹ��������ѧУѡ�������ʡǮ�ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У���BAC=90��AB=AC���ֱ����B��C��������A��ֱ�ߵĴ���BD��CE����BD=14cm��CE=3cm����DE=_____
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����8�֣�Ϊ�˹᳹��ʵ��ί�и������������ƶ������ijУ���ƶ���һϵ�й��ڰ��A��B��ƶ����ļƻ����־�����ij������152�����絽A��B������ֳ�����ô�С������15������ǡ����һ���������������磬��֪�����ִ�С�������ػ������ֱ�Ϊ12��/����8��/����������A��B������˷����±���

��1������15�����д�С��������������
��2���ְ�������10������ǰ��A�壬�������ǰ��B�壬��ǰ��A��Ĵ����Ϊx����ǰ��A��B�����ܷ���ΪyԪ�������y��x�ĺ�������ʽ��
��3���ڣ�2���������£�������A������粻����100�䣬����д��ʹ�ܷ������ٵĻ������䷽������������ٷ��ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
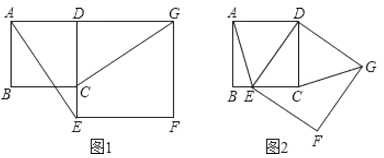
����Ŀ����ͼ1����֪������ABCD�ı�CD��������DEFG�ı�DE�ϣ�����AE��GC��
��1���Բ���AE��GC�������Ĺ�ϵ����֤����Ľ��ۣ�
��2����������DEFG�Ƶ�D��˳ʱ�뷽����ת��ʹ��E����BC���ϣ���ͼ2������AE��CG������Ϊ��1���еĽ����Ƿ�����������������֤����������������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һԪ���η���x2��4x+k=0����������ȵ�ʵ����
��1����k��ȡֵ��Χ��
��2�����k�Ƿ��������������������һԪ���η���x2��4x+k=0��x2+mx��1=0��һ����ͬ�ĸ������ʱm��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y=ax+b��a��0�������κ���y=ax2+bx�ͷ���������y=![]() ��k��0����ͬһֱ������ϵ�е�ͼ����ͼ��ʾ��A�������Ϊ��-2��0���������н����У���ȷ���ǣ�������
��k��0����ͬһֱ������ϵ�е�ͼ����ͼ��ʾ��A�������Ϊ��-2��0���������н����У���ȷ���ǣ�������

A��b=2a+k B��a=b+k C��a��b��0 D��a��k��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ߺ������������й�������Ĺ�·����·�������������Ų��õ���б�������ͣ����ͼ����ͼ���Ǵ�ͼ���������ƽ��ͼ��������վ�����ϲ������AB��ˮƽ����ļн���30��������CD��ˮƽ����ļн���60�������������˵ľ���BCΪ2�ף��������˾���ADΪ20�ף����������BH�ij����������ȷ��0.1�ף� ![]() ��1.732��
��1.732��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com