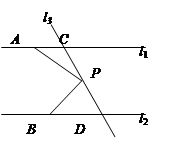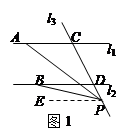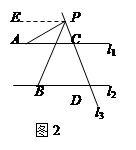试题分析:解:若P点在C、D之间运动时,则有∠APB=∠PAC+∠PBD.理由是:如图4,过点P作PE∥
l1,则∠APE=∠PAC,又因为l
1∥l
2,所以PE∥l
2,所以∠BPE=∠PBD,所以∠APE+∠BPE=∠PAC+∠PBD,即∠APB=∠PAC+∠PBD.
若点P在C、D两点的外侧运动时(P点与点C、D不重合),则有两种情形:
(1)如图1,有结论:∠APB=∠PBD-∠PAC.理由是:过点P作PE∥l
1,则∠APE=∠PAC,又因为l
1∥l
2,所以PE∥l
2,所以∠BPE=∠PBD,所以∠APB=∠BAE+∠APE,即∠APB=∠PBD-∠PAC.
(2)如图2,有结论:∠APB=∠PAC-∠PBD.理由是:过点P作PE∥l
2,则∠BPE=∠PBD,又因为l
1∥l
2,所以PE∥
l1,所以∠APE=∠PAC,所以∠APB=∠APE+∠BPE,即∠APB=∠PAC+∠PBD.
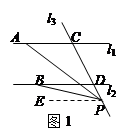
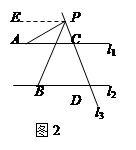
点评:本题难度较大,主要考查学生结合平行线性质及动点性质综合运用解题能力,动点为中考几何大题常考题型,要求学生注意培养数形结合思想,灵活运用到考试中去。