
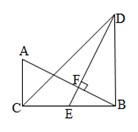
如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为点
F,且AB=DE。(1)求证:BD=BC;(2)若BD=8cm,求AC的长。
科目:初中数学 来源: 题型:
(1)动手操作:
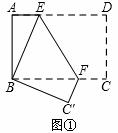
如图①,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点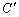 处,折痕为EF,若∠ABE=20°,那么∠
处,折痕为EF,若∠ABE=20°,那么∠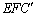 的度数为____________.
的度数为____________.
(2)观察发现:
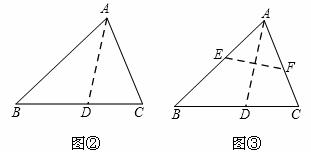
小明将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图②);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图③).小明认为△AEF是等腰三角形,你同意吗?请说 明理由.
明理由.
(3)实践与运用:
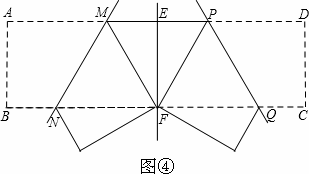
将矩形纸片ABCD 按如下步骤操作:将纸片对折得折痕EF,折痕与AD边交于点E,与BC边交于点F;将矩形ABFE与矩形EFCD分别沿折痕MN和PQ折叠,使点A、点D都与点F重合,展开纸片,此时恰好有MP=MN=PQ(如图④),求∠MNF的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
为了落实国家的惠农政策,某地政府制定了农户投资购买收割机的补贴办法,其中购买Ⅰ、Ⅱ两型收割机所投资的金额与政府补贴的额度存在下表所示的函数对应关系:
| Ⅰ型收割机 | Ⅱ型收割机 | ||||
| 投资金额x(万元) | x | 5 | x | 2 | 4 |
| 补贴金额y(万元) | y1=kx | 2 | y2=ax2+bx | 2.4 | 3.2 |
(1)分别求出y1和y2的函数表达式;
(2)旺叔准备投资10万元购买Ⅰ、Ⅱ两型收割机。请你设计一个能获得最大补贴金额的
方案,并求出按此方案能获得的补贴金额。
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙两班学生植树造林,已知甲班每天比乙班多植5棵树,甲班植80棵树所用的天数与乙班植70棵树所用的天数相等,若设甲班每天植树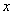 棵,则根据题意列出方程是( )
棵,则根据题意列出方程是( )
A.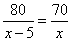 B.
B.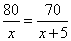 C.
C.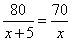 D.
D.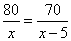
查看答案和解析>>
科目:初中数学 来源: 题型:
一个钢筋三角 架三边长分别为20cm,50cm,60cm,现要再做一个与其相似的钢筋三角架,而只有长为30cm和50cm的两根钢筋,要求以其中的一根为一边,从另一根截下两段(允许有余料)作为另两边,则不同的截法有(
架三边长分别为20cm,50cm,60cm,现要再做一个与其相似的钢筋三角架,而只有长为30cm和50cm的两根钢筋,要求以其中的一根为一边,从另一根截下两段(允许有余料)作为另两边,则不同的截法有( )
)
A.一种 B.两种 C.三种 D.四种
查看答案和解析>>
科目:初中数学 来源: 题型:
准备两张大小一样,分别画有不同图案的正方形纸片,把每张纸都对折、剪开,
将四张纸片放在盒子里,然后混合,随意抽出两张正好能拼成原 图的概率是( )
图的概率是( )
A.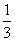 B.
B.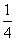 C.
C.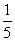 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,
垂足为E,ED的延长线与AC的延长线交于点F。
(1)求证:DE是⊙O的切线;
 (2)若⊙O的半径为2,BE=1,求cosA的值.
(2)若⊙O的半径为2,BE=1,求cosA的值.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com