
【题目】在《九章算术》中有求三角形面积公式“底乘高的一半”,但是在实际丈量土地面积时,量出高并非易事,所以古人想到了能否利用三角形的三条边长来求面积.我国南宋著名的数学家秦九韶(![]() 年—
年—![]() 年)提出了“三斜求积术”,阐述了利用三角形三边长求三角形面积方法,简称秦九韶公式.在海伦(公元
年)提出了“三斜求积术”,阐述了利用三角形三边长求三角形面积方法,简称秦九韶公式.在海伦(公元![]() 年左右,生平不详)的著作《测地术》中也记录了利用三角形三边长求三角形面积的方法,相传这个公式最早是由古希腊数学家阿基米德(公元前
年左右,生平不详)的著作《测地术》中也记录了利用三角形三边长求三角形面积的方法,相传这个公式最早是由古希腊数学家阿基米德(公元前![]() 年—公元前
年—公元前![]() 年)得出的,故我国称这个公式为海伦一秦九韶公式.它的表达为:三角形三边长分别为
年)得出的,故我国称这个公式为海伦一秦九韶公式.它的表达为:三角形三边长分别为![]() 、
、![]() 、
、![]() ,则三角形的面积
,则三角形的面积![]() (公式里的
(公式里的![]() 为半周长即周长的一半).
为半周长即周长的一半).
请利用海伦一秦九韶公式解决以下问题:
(![]() )三边长分别为
)三边长分别为![]() 、
、![]() 、
、![]() 的三角形面积为__________.
的三角形面积为__________.
(![]() )四边形
)四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 的面积为__________.
的面积为__________.
(![]() )五边形
)五边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,五边形
,五边形![]() 的面积为__________.
的面积为__________.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,乙厂直接按印刷数量收取印刷费.甲乙两厂的印刷费用y(千元)与证书数量x(千个)的函数关系图象分别如图中甲、乙所示.

(1)填空:甲厂的制版费是________千元,当x≤2(千个)时乙厂证书印刷单价是________元/个;
(2)求出甲厂的印刷费y甲与证书数量x的函数关系式,并求出其证书印刷单价;
(3)当印制证书8千个时,应选择哪个印刷厂节省费用,节省费用多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于![]() 的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=kx+b与反比例函数y=![]() (x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(1)求直线AB的解析式;
(2)若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在平面直角坐标系
,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,连接
,连接![]() .
.
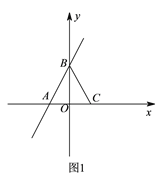
(![]() )求证:
)求证:![]() 是等边三角形.
是等边三角形.
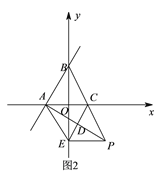
(![]() )点
)点![]() 在线段
在线段![]() 的延长线上,连接
的延长线上,连接![]() ,作
,作![]() 的垂直平分线,垂足为点
的垂直平分线,垂足为点![]() ,并与
,并与![]() 轴交于点
轴交于点![]() ,分别连接
,分别连接![]() 、
、![]() .
.
①如图![]() ,若
,若![]() ,直接写出
,直接写出![]() 的度数.
的度数.
②若点![]() 在线段
在线段![]() 的延长线上运动(
的延长线上运动(![]() 与点
与点![]() 不重合),
不重合),![]() 的度数是否变化?若变化,请说明理由;若不变,求出
的度数是否变化?若变化,请说明理由;若不变,求出![]() 的度数.
的度数.
(![]() )在(
)在(![]() )的条件下,若点
)的条件下,若点![]() 从点
从点![]() 出发在
出发在![]() 的延长线上匀速运动,速度为每秒
的延长线上匀速运动,速度为每秒![]() 个单位长度,
个单位长度,![]() 与
与![]() 交于点
交于点![]() ,设
,设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() ,运动时间为
,运动时间为![]() 秒时.求
秒时.求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y1=![]() x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.
x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.
(1)求两直线交点D的坐标;
(2)求△ABD的面积;
(3)根据图象直接写出y1>y2时自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现定义一种新运算:“※”,使得a※b=4ab
(1)求4※7的值;
(2)求x※x+2※x﹣2※4=0中x的值;
(3)不论x是什么数,总有a※x=x,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.袋中有形状、大小、质地完全一样的5个红球和1个白球,从中随机抽出一个球,一定是红球
B.天气预报“明天降水概率10%”,是指明天有10%的时间会下雨
C.某地发行一种福利彩票,中奖率是千分之一,那么,买这种彩票1000张,一定会中奖
D.连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com