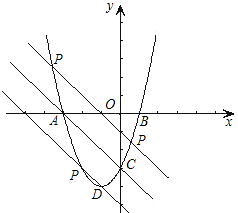
已知:抛物线y=x2+2x-3与x轴的两个交点分别为A、B,点A在点B的左侧,与y轴交于点C,顶点为D,直线y=kx+b经过点A、C;
(1)求点D的坐标和直线AC的解析式;
(2)点P为抛物线上的一个动点,求使得△ACP的面积与△ACD的面积相等的点P的坐标.
解:(1)由抛物线解析式y=x
2+2x-3=(x+1)
2-4,
得D(-1,-4);
点A、C的坐标分别是A(-3,0),C(0,-3),
∵直线y=kx+b经过A、C两点,
∴
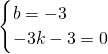
,
∴
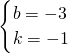
;
∴直线AC的解析式为y=-x-3;
(2)①过点D作与直线y=-x-3平行的直线,交抛物线于点P;
则S
△ACP=S
△ACD;
设平移后的直线的解析式为y=-x+t,
∵点D的坐标为(-1,-4);
∴t=-5;
∴P(m,-m-5),
∴-m-5=m
2+2m-3,
解得m=-1(舍去)或m=-2;
∴P(-2,-3);
②直线DP:y=-x-5与y轴的交点坐标为(0,-5),
则直线DP关于直线y=-x-3对称的直线l的解析式为y=-x-1,l交抛物线于P′,设P′(m′,-m′-1);
由于点P’在抛物线y=x
2+2x-3上,
∴-m′-1=m′
2+2m′-3;
解得
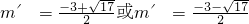
;
∴P′(
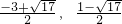
)或P′(
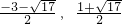
);
∴所求点P的坐标分别是(-2,-3),(
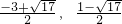
),(
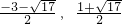
).
分析:(1)根据抛物线的解析式,可求出点A、C、D的坐标,进而可用待定系数法求出直线AC的解析式;
(2)由于△ACP和△ACD同底,若它们的面积相等,则点P到AC的距离等于点D到AC的距离;过点D作直线AC的平行线,那么此平行线与抛物线的交点必为所求的P点;设直线DP关于直线AC对称的直线为l,那么直线l和直线AC的距离也等于D到AC的距离,因此直线l与抛物线的交点也符合点P的要求,所以点P的坐标共有3个,可先求出直线DP和直线l的解析式,然后联立抛物线的解析式即可求出P点的坐标.
点评:此题主要考查了二次函数图象与坐标轴交点以及顶点坐标的求法、一次函数解析式的确定、三角形面积的求法以及函数图象交点坐标的求法等重要知识,同时还考查了分类讨论的数学思想,难度偏大.

 解:(1)由抛物线解析式y=x2+2x-3=(x+1)2-4,
解:(1)由抛物线解析式y=x2+2x-3=(x+1)2-4,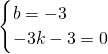 ,
,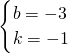 ;
;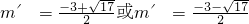 ;
;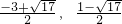 )或P′(
)或P′(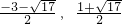 );
);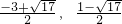 ),(
),(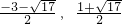 ).
).

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案