
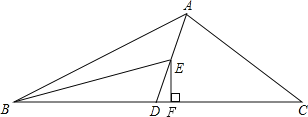
【题目】如图,AD为△ABC的中线,BE为三角形ABD中线,
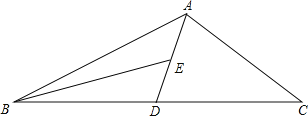
(1)∠ABE=15°,∠BAD=35°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为60,BD=5,则点E到BC边的距离为多少?
【答案】(1)50°(2)见解析;(3)6
【解析】
试题分析:(1)利用三角形的外角等于与它不相邻的两个内角之和即可求∠BED的度数;
(2)△BED是钝角三角形,所以BD边上的高在BD的延长线上;
(3)先根据三角形的中线把三角形分成面积相等的两个小三角形,结合题意可求得△BED的面积,再直接求点E到BC边的距离即可.
解:(1)∵∠BED是△ABE的一个外角,
∴∠BED=∠ABE+∠BAD=15°+35°=50°.
(2)如图所示,EF即是△BED中BD边上的高.
(3)∵AD为△ABC的中线,BE为三角形ABD中线,
∴S△BED=![]() S△ABC=
S△ABC=![]() ×60=15;
×60=15;
∵BD=5,
∴EF=2S△BED÷BD=2×15÷5=6,
即点E到BC边的距离为6.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中, A(0,4),B(-3,0).
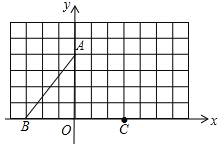
(1)①画出线段AB关于y轴对称线段AC;
②将线段AC绕点C顺时针旋转一个角,得到对应线段CD,使得AD//x轴,请画出线段CD;
(2)判断四边形ABCD的形状 ;
(3)若直线![]() 平分四边形ABCD的面积,请直接写出实数k的值.
平分四边形ABCD的面积,请直接写出实数k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴交与A(4,0),并且OA=OC=4OB,点P为过A、B、C三点的抛物线上一动点.
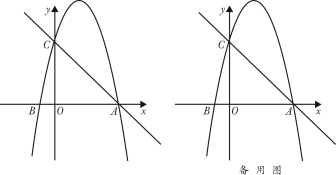
(1)、求点B、点C的坐标并求此抛物线的解析式;
(2)、是否存在点P,使得△ACP是以点C为直角顶点的直角三角形?若存在,求出点P的坐标;若不存在,说明理由;
(3)、过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距S千米,某人行完全程所用的时间t(时)与他的速度v(千米/时)满足vt=S,在这个变化过程中,下列判断中错误的是 ( )
A.S是变量 B.t是变量 C.v是变量 D.S是常量
查看答案和解析>>
科目:初中数学 来源: 题型:
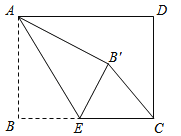
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为_____ ____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌商品,按标价八折出售,仍可获得10%的利润.若该商品标价为275元,则商品的进价为( )
A. 192.5元 B. 200元 C. 244.5元 D. 253元
查看答案和解析>>
科目:初中数学 来源: 题型:
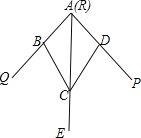
【题目】如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )
A.SAS B.ASA C.AAS D.SSS
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com