
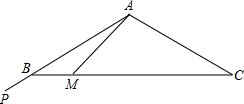
 在一次科技活动中,小明进行了模拟雷达扫描实验.如图,表盘是△ABC,其中AB=AC,∠BAC=120°,在点A处有一束红外光线AP,从AB开始,绕点A逆时针匀速旋转,每秒钟旋转15°,到达AC后立即以相同旋转速度返回AB,到达后立即重复上述旋转过程.小明通过实验发现,光线从AB处旋转开始计时,旋转1秒,此时光线AP交BC边于点M,BM的长为(20
在一次科技活动中,小明进行了模拟雷达扫描实验.如图,表盘是△ABC,其中AB=AC,∠BAC=120°,在点A处有一束红外光线AP,从AB开始,绕点A逆时针匀速旋转,每秒钟旋转15°,到达AC后立即以相同旋转速度返回AB,到达后立即重复上述旋转过程.小明通过实验发现,光线从AB处旋转开始计时,旋转1秒,此时光线AP交BC边于点M,BM的长为(20| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
80
| ||
| 3 |
| 3 |
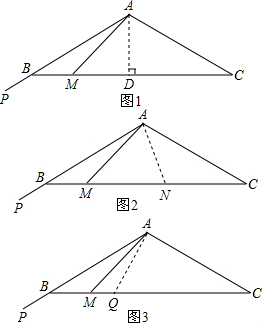 解:(1)如图1,过A点作AD⊥BC,垂足为D.
解:(1)如图1,过A点作AD⊥BC,垂足为D.| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 3 |
| AB |
| cos30° |
| 40 | ||||
|
80
| ||
| 3 |
80
| ||
| 3 |
80
| ||
| 3 |
| ||
| 2 |
| 3 |
| 3 |
80
| ||
| 3 |
40
| ||
| 3 |
40
| ||
| 3 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
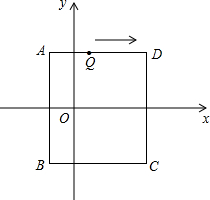 如图,在平面直角坐标系中,长方形ABCD的边BC∥x轴.如果A点坐标是(-1,2
如图,在平面直角坐标系中,长方形ABCD的边BC∥x轴.如果A点坐标是(-1,2| 2 |
| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 西瓜质量(单位:千克) | 5.4 | 5.3 | 5.0 | 4.8 | 4.4 | 4.0 |
| 西瓜数量(单位:个) | 1 | 2 | 3 | 2 | 1 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com