
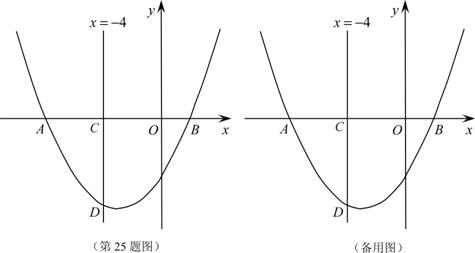
如图,已知抛物线![]() 经过A(-8,0),B(2,0)两点,直线
经过A(-8,0),B(2,0)两点,直线![]() 交
交 ![]() 轴于点C,交抛物线于点D.
轴于点C,交抛物线于点D.
(1)求该抛物线的解析式;
(2)点P在抛物线上,点E在直线![]() 上,若以A,O,E,P为顶点的四边形是平行四边形,求点P的坐标;
上,若以A,O,E,P为顶点的四边形是平行四边形,求点P的坐标;
(3)若B,D,C三点到同一条直线的距离分别是![]() ,
,![]() ,
,![]() ,问是否存在直线l,使
,问是否存在直线l,使![]() ?若存在,请直接写出
?若存在,请直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
数学试卷参考答案及评分说明
解:(1)∵抛物线![]() 经过A(-8,0),B(2,0)两点,
经过A(-8,0),B(2,0)两点,
∴![]() , 解得:
, 解得:![]() ··········· 2分
··········· 2分
∴![]() ;
;![]() ··················· 3分
··················· 3分
(2)∵点P在抛物线上,点E在直线![]() 上,
上,
设点P的坐标为![]() ,
,![]() ,点E的坐标为
,点E的坐标为![]() ,
,![]() .
.
如图1,∵点A(-8,0),∴![]() .
.
①当AO为一边时,EP∥AO, 且![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,![]() .
.
∴P1(![]() ,14),P2(4,6) ·················· 5分
,14),P2(4,6) ·················· 5分
②当AO为对角线时,则点P和点E必关于点C成中心对称,故![]() .
.
∴ 解得:
解得:![]() ∴P3 (
∴P3 (![]() ,
,![]()
![]() ).
).
∴当P1(![]() ,14),P2(4,6),P3 (
,14),P2(4,6),P3 (![]() ,
,![]() )时,A,O,E,P为顶点
)时,A,O,E,P为顶点
的四边形是平行四边形. ··················· 7分
(3)存在直线![]() ,使
,使![]() . ················ 8分
. ················ 8分
![]() 的值为:
的值为:![]() ,
,![]() ,
,![]() ,
,![]() .·········· 12分
.·········· 12分
 |
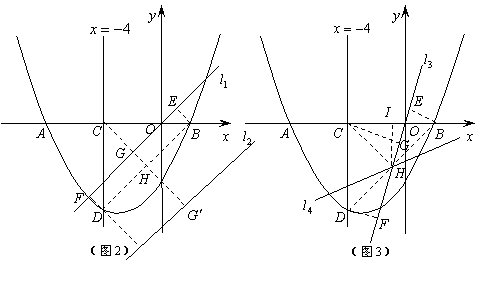 |
附25.(3)参考答案:
解:存在直线![]() 使
使![]() .连BD.过
.连BD.过![]() 点C作CH⊥BD于点H.(如图2)
点C作CH⊥BD于点H.(如图2)
![]() 由题意得C(-4,0) ,B(2,0) ,D(-4,-6),
由题意得C(-4,0) ,B(2,0) ,D(-4,-6),
∴OC=4 ,OB=2,CD=6.∴△CDB为等腰直角三角形.
∴CH=CD![]() ,即:
,即:![]() .
.
∵BD=2CH,∴BD=![]() .
.
①∵CO:OB=2:1,∴过点O且平行于BD的直线满足条件
作BE⊥直线![]() 于点E ,DF⊥直线
于点E ,DF⊥直线![]() 于点F,设CH交直线
于点F,设CH交直线![]() 于点G.
于点G.
∴![]() ,即:
,即:![]() .
.
则![]() ,
, ![]() ,即
,即![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∴![]() ,即
,即![]() .
.
②如图2,在△CDB外作直线l2平行于DB,延长CH交l2于点G′,
使![]() , ∴
, ∴![]() .
.
③如图3,过H,O作直线![]() ,作BE⊥
,作BE⊥![]() 于点E,DF⊥
于点E,DF⊥![]() 于点F,CG⊥
于点F,CG⊥![]() 于点G,由①可知,
于点G,由①可知,![]()
则![]() ,即
,即![]() :
:![]() .
.
∵CO:OB=2:1,∴![]() .
.
作HI⊥![]() 轴于点I,
轴于点I,
∴HI= CI=![]() =3. ∴OI=4-3=1,
=3. ∴OI=4-3=1,
∴![]() .
.
∵△OCH的面积=![]() ,∴
,∴![]() .
.
④如图3,根据等腰直角三角形的对称性,可作出直线![]() ,易证:
,易证:
![]() ,
,![]() .
.
∴存在直线![]() ,使
,使![]() .
.![]() 的值为:
的值为:![]() ,
,![]() ,
,![]() ,
,![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
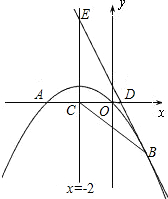 2x+1经过抛物线上一点B(2,m),且与y轴.直线x=-2分别交于点D、E.
2x+1经过抛物线上一点B(2,m),且与y轴.直线x=-2分别交于点D、E.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E,
如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E,查看答案和解析>>
科目:初中数学 来源: 题型:
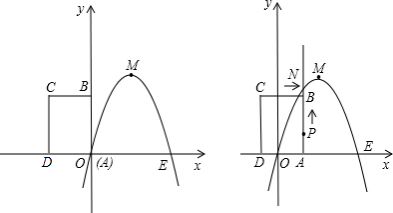
 如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),
如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com