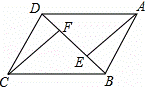
如图，AB∥CD，BC∥AD，AE∥CF，则图中全等三角形有（ ）
|
| A． | 3对 | B． | 4对 | C． | 5对 | D． | 6对 |
|
|
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
如图，要
从△ABC得到△DEF，需（ ）．
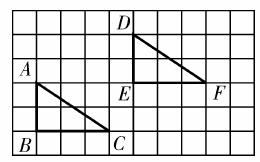
A．把△ABC向左平移4个单位，再向下平移2个单位
B．把△ABC向右平移4个单位，再向下平移2个单位
C．把△ABC向右平移4个单位，再向上平移2个单位
D．把△ABC向左平移4个单位，再向上平移2个单位
查看答案和解析>>
科目：初中数学 来源： 题型：
古运河是扬州的母亲河，为
打造古运河风光带，现有一段长为180m的河道整治任务由A、B 两工程队先后接力完成，A工程队每天整治12m，B 工程队每天整治8m，共用时20天．
（1）根据题意，甲、乙两名同学分别列出尚不完整的方程组如下：
根据甲、乙两名同学所列的方程组，请你分别指出未知数x，y表示的意义，然后在方框中补全甲、乙两名同学所列的方程组：
甲：x表示___________，y表示___________；
乙：x表示___________，y表示___________；
（2）A、B两工程队分别
整治河道多少米？（写出完整的解答过程）
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，E、F是平行四边形对角线AC上的两点，并且AE＝CF．求证：四边形BFDE是平行四边形．判定平行四边形的方法很多，在具体应用时，到底
用哪种方法更好呢？
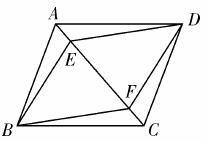
小明、小华、小
颖三位同学对此题进行探讨，给出了各自不同的证明如下：
小明的证明方法：
∵ 四边形ABCD是平行四边形，
∴ AD∥BC，AD＝BC．
∴ ∠DAE＝∠BCF．
又 AE＝CF，
∴ △AED≌△CFB．
∴ DE＝BF，∠AED＝∠CFB．
∴ ∠DEF＝∠BFE．
∴ 
ED∥BF．
∴ 四边形BEDF是平行四边形．
小华的证明方法：
∵ 四边形ABCD是平行四边形，
∴ AD∥BC，AD＝BC．
∴ ∠DAE＝∠BCF．
又 AE＝CF，
∴ △AED≌△CFB．
∴ DE＝BF．
同理可证△ABE≌△CDF．
∴ BE＝DF．
∴ 四边形BEDF是平行四边形．
小颖的证明方法：
如图，连接BD交AC于点O．
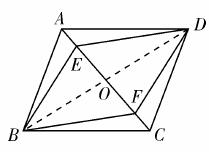
∵ 四边形ABCD是平行四边形，
∴ AO＝OC，BO＝OD．
又 AE＝CF，
∴ OE＝OF．
由BO＝OD，OE＝OF知四边形BEDF是平行四边形．
就这三名同学的证明方法，你认为哪一种方法最为简捷？从中你得到什么启示？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
