
如图,Rt△ABC中,∠C=90°,∠ABC=30°,AB=6.点D在AB边上,点E是BC边上一点(不与点B、C重合),且DA=DE,则AD的取值范围是________________.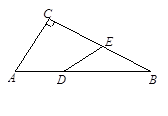
2≤AD<3
解析试题考查知识点:动点问题
思路分析:考虑到AD=DE且都过D点,故做以D为圆心、AD为半径的圆,以期得出结果
具体解答过程:
∵Rt△ABC中,∠C=90°,∠ABC=30°,AB=6
∴AC=AB·sin∠ABC=6×sin30°=3
当D、E在如下图所示的位置时,AD最短。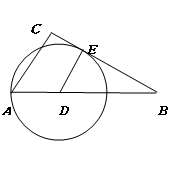
不妨设DE=AD=x,此时BC是以AD长为半径的⊙D的切线,DE⊥BC,DE∥AC,Rt△BCA∽Rt△BED,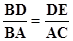
∵AB=6,AC=3,BD=6-x
∴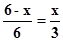 即x=2
即x=2
∴DE=AD=2
当D、E在如下图所示的位置时,AD最长。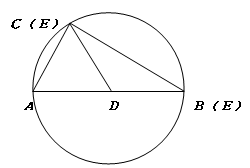
此时,△ABC为以AD长为半径的⊙D的内接三角形,DE=AD=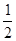 AB=3
AB=3
综上所述,并考虑到点E不与点B、C重合,可知AD的取值范围是:
2≤AD<3
试题点评:利用圆来解决三角形的问题,也是一种很好的思路。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,Rt△ABC中,∠ACB=90°,tanB=
如图,Rt△ABC中,∠ACB=90°,tanB=| 3 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.
如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com