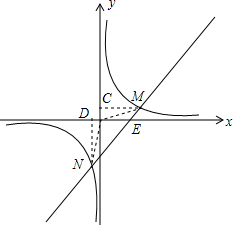
解:(1)∵点M(2,1)在反比例函数y=

的图象上,
∴m=2×1=2,
∴反比例函数的解析式为:y=

;
∵点M(2,1)在一次函数y=2x+n的图象上,
∴4+n=1,解得n=-3,
∴一次函数y=2x+n的解析式为y=2x-3,
∴

,
解得

或
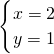
,
∴N(-

,-4);
(2)∵一次函数y=kx+b的解析式为y=2x-3,
∴E(

,0),
∵M(2,1),N(-

,-4),
∴S
△MON=S
△MOE+S
△NOE=

×

×1+

×

×4=5;
(3)平行.
证明:∵M(2,1),N(-

,-4),
∴C(0,1),D(-

,0),
设直线CD的解析式为y=ax+b,则
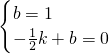
,
解得

,
∴直线CD的解析式为;y=2x+1,
∵一次函数y=2x+n的解析式为y=2x-3,
∴直线CD与直线MN平行.
分析:(1)先根据M点的坐标求出m的值,进而得出反比例函数的解析式,再把M点的坐标代入一次函数的解析式即可得出n的值即可得出一次函数的解析式,把一次函数与反比例函数的解析式联立即可得出N点坐标;
(2)先根据n的值得出一次函数的解析式,求出一次函数与x轴的交点坐标,由S
△MON=S
△MOE+S
△NOE即可得出结论;
(3)根据xy轴上点的坐标特点求出过C、D两点的直线解析式,再与已知直线的解析式相比较即可.
点评:本题考查的是反比例函数与一次函数的交点问题,涉及到用待定系数法求一次函数及反比例函数的解析式,根据题意得出m的值是解答此题的关键.

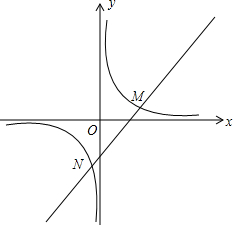 已知一次函数y=2x+n与反比例函数
已知一次函数y=2x+n与反比例函数 的图象相交于M、N两点,且M为(2,1)
的图象相交于M、N两点,且M为(2,1) 解:(1)∵点M(2,1)在反比例函数y=
解:(1)∵点M(2,1)在反比例函数y= 的图象上,
的图象上, ;
; ,
, 或
或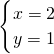 ,
, ,-4);
,-4); ,0),
,0), ,-4),
,-4), ×
× ×1+
×1+ ×
× ×4=5;
×4=5; ,-4),
,-4), ,0),
,0),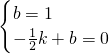 ,
, ,
,

 阅读快车系列答案
阅读快车系列答案