
【题目】已知在四边形![]() 中,∠A=∠C=90°.
中,∠A=∠C=90°.
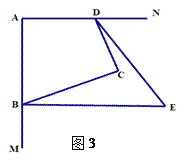
(1)如图1,若BE平分∠ABC,DF平分∠ADC的邻补角,请写出BE与DF的位置关系,并证明.

(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证明.

(3)如图3,若BE、DE分别五等分∠ABC、∠ADC的邻补角(即∠CDE=![]() ,∠CBE=
,∠CBE=![]() ),则∠E= .
),则∠E= .
【答案】(1)见解析;(2)见解析;(3)54°
【解析】分析:(1)延长BE、FD交于G.由四边形ABCD内角和为360°及邻补角定义,可得到∠ABC=∠CDN.由角平分线性质得到∠ABE=∠FDN,进一步得到∠ABE=∠GDE,由三角形内角和定理可得结论.
(2)连接DB.由四边形ABCD内角和为360°及邻补角定义,可得到∠MBC+∠CDN=180°.由角平分线性质得到∠CBF+∠CDE=90°,进一步得到∠EDB+∠DBF=180°,由平行线的判定可得结论.
(3)延长DC交BE于H.先求出∠CDE+∠CBE,再根据三角形的一个外角等于与它不相邻的两个内角的和求解即可.
详解: (1) BE⊥DF .证明如下:
延长BE、FD交于G.在四边形ABCD中,∵∠A+∠ABC+∠C+∠ADC=360°,∠A=∠C=90°,∴∠ABC+∠ADC=180°.
又∵∠ADC+∠CDN=180°,∴∠ABC=∠CDN.
∵BE平分∠ABC,DF平分∠CDN,∴∠ABE=![]() ∠ABC,∠FDN=
∠ABC,∠FDN=![]() ∠CDN,∴∠ABE=∠FDN.
∠CDN,∴∠ABE=∠FDN.
又∵∠FDN=∠GDE,∴∠ABE=∠GDE.
又∵∠AEB=∠GED,∴∠A=∠G=90°,∴BE⊥DF.
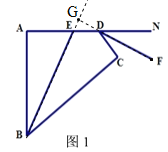
(2)DE∥BF.证明如下:
连接DB.∵∠ABC+∠MBC=180°,∠ADC+∠CDN=180°.
又∵∠ABC+∠ADC=180°,∴∠MBC+∠CDN=180°.
∵BF、DE平分∠ABC、∠ADC的邻补角,∴∠CBF=![]() ∠MBC,∠CDE=
∠MBC,∠CDE=![]() ∠CDN,∴∠CBF+∠CDE=90°.
∠CDN,∴∠CBF+∠CDE=90°.
在Rt△BDC中,∵∠CDB+∠DBC=90°,∴∠CDB+∠DBC+∠CBF+∠CDE=180°,∴∠EDB+∠DBF=180°,∴DE∥BF.
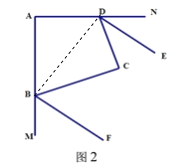
(3)延长DC交BE于H.由(1)得:∠CDN+∠CBM=180°.∵BE、DE分别五等分∠ABC、∠ADC的外角,∴∠CDE+∠CBE=![]() ×180°=36°,由三角形的外角性质得,∠BHD=∠CDE+∠E,∠BCD=∠BHD+∠CBE,∴∠BCD=∠CBE+∠CDE+∠E,∴∠E=90°﹣36°=54°.
×180°=36°,由三角形的外角性质得,∠BHD=∠CDE+∠E,∠BCD=∠BHD+∠CBE,∴∠BCD=∠CBE+∠CDE+∠E,∴∠E=90°﹣36°=54°.


科目:初中数学 来源: 题型:
【题目】已知直线l1:y1=2x+3与直线l2:y2=kx﹣1相交于点A,A横坐标为﹣1,且直线l1与x轴交于B点,与y轴交于D点,直线l2与y轴交于C点.
(1)求出A点的坐标及直线l2的解析式;
(2)连接BC,求出S△ABC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知边长为m的正方形面积为12,则下列关于m的说法中,错误的是( )
①m是无理数;②m是方程m2 -12=0的解;③m满足不等式组![]() ,④m是12的算术平方根.
,④m是12的算术平方根.
A. ①② B. ①③ C. ③ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F. 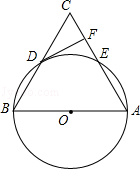
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求 ![]() 的长(结果保留π).
的长(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在,苏宁商场进行促销活动,出售一种优惠购物卡(注:此卡只作为购物优惠凭证不能顶替货款),花300元买这种卡后,凭卡可在这家商场按标价的8折购物.
(1)顾客购买多少元金额的商品时,买卡与不买卡花钱相等?在什么情况下购物合算?
(2)小张要买一台标价为3500元的冰箱,如何购买合算?小张能节省多少元钱?
(3)小张按合算的方案,把这台冰箱买下,如果商场还能盈利25%,这台冰箱的进价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“我最喜爱的老师”评选活动.确定如下评选方案:有学生和教师代表对4名候选教师进行投票,每票选1名候选教师,每位候选教师得到的教师票数的5倍与学生票数的和作为该教师的总票数.以下是根据学生和教师代表投票结果绘制的统计表和条形统计图(不完整). 学生投票结果统计表
候选教师 | 丁老师 | 俞老师 | 李老师 | 陈老师 |
得票数 | 200 | 300 |
(1)若共有25位教师代表参加投票,则李老师得到的教师票数是多少?请补全条形统计图.(画在答案卷相对应的图上)
(2)丁老师与李老师得到的学生总票数是600,且丁老师得到的学生票数是李老师得到的学生票数的3倍多40票,求丁老师与李老师得到的学生票数分别是多少?
(3)在(1)、(2)的条件下,若总得票数较高的2名教师推选到市参评,你认为推选到市里的是两位老师?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
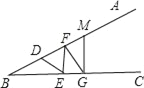
【题目】已知:如图,BD=DE=EF=FG.
(1)若∠ABC=20°,∠ABC内符合条件BD=DE=EF=FG的折线(如DE、EF、FG)共有几条?若∠ABC=10°呢?试一试,并简述理由.
(2)若∠ABC=m°(0<m<90),你能找出一个折线条数n与m之间的关系吗?若有,请找出来;若无,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
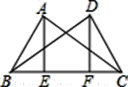
【题目】如图所示,△ABC和△DCB有公共边BC,且AB=DC,作AE⊥BC,DF⊥BC,垂足分别为E、F,AE=DF,那么求证AC=BD时,需要证明三角形全等的是Rt△ABE≌Rt△DCF,△AEC≌DFB.说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com