
【题目】如图所示,CE⊥AB于点E,BD⊥AC于点D,BD,CE交于点O,且AO平分∠BAC,则图中的全等三角形共有________对.

【答案】4
【解析】
根据题目条件,全等三角形有:△ABO≌△ACO,△AEC≌△ADB,△AEO≌△ADO,△BEO≌△CDO共4对.解题时要根据已知条件结合判定方法逐个验证,做到由易到难,不重不漏.
①在△AEO与△ADO中
∵CE⊥AB于点E,BD⊥AC于点D,AO平分∠BAC,
∴∠AEO=∠ADO=90°,∠EAO=∠DAO
∵AO=AO
∴△AEO≌△ADO(AAS)
∴AE=AD,OE=OD;
②在△OBE与△OCD中
∵∠OEB=∠0DC=90°,∠EOB=∠DOC,OE=OD
∴△OBE≌△OCD(AAS)
∴OB=OC,BE=DC,∠B=∠C;
③在△ABO与△ACO中
∵AE=AD
∴AB=AC
∵AB=AC,AO=AO,BO=CO
∴△ABO≌△ACO(SSS)
④在△AEC与△ADB中
∵∠AEC=∠ADB=90°,AC=AB,AE=AD
∴△AEC≌△ADB(HL)
所以共有4对全等三角形.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.
(1)求每张门票的原定票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠政策,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在四边形![]() 中,∠A=∠C=90°.
中,∠A=∠C=90°.
(1)如图1,若BE平分∠ABC,DF平分∠ADC的邻补角,请写出BE与DF的位置关系,并证明.

(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证明.

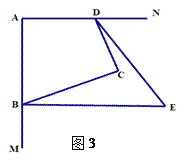
(3)如图3,若BE、DE分别五等分∠ABC、∠ADC的邻补角(即∠CDE=![]() ,∠CBE=
,∠CBE=![]() ),则∠E= .
),则∠E= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形都是由同样大小的正方形按照一定规律所组成的,其中第①个图形中一个有2个正方形,第②个图形中一共有8个正方形,第③个图形中一共有16个正方形,…,按此规律,第⑦个图形中正方形的个数为( )

A. 56 B. 65 C. 68 D. 71
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C、D、E在同一直线上,且AC=BD,E是线段BC的中点.
![]()
(1)点E是线段AD的中点吗?说明理由;
(2)当AD=10,AB=3时,求线段BE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的个数是( )
(1)﹣a表示负数;
(2)多项式﹣3a2b+7a2b2﹣2ab+l的次数是3;
(3)单项式﹣![]() 的系数为﹣2;
的系数为﹣2;
(4)一个有理数不是整数就是分数
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是经过∠BCA的顶点C的一条直线,CA=CB,E,F是直线CD上的两点,且∠BEC=∠CFA=α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图(a),若∠BCA=90°,α=90°,则BE________CF,EF________|BE-AF|(填“>”“<”或“=”);
②如图(b),若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件________,使①中的两个结论仍然成立,并证明两个结论成立;
(2)如图(c),若直线CD经过∠BCA的外部,∠BCA=α,请写出EF,BE,AF三条线段数量关系的合理猜想(不要求证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF. 
(1)求证:AB是⊙O的切线;
(2)若CF=4,DF= ![]() ,求⊙O的半径r及sinB.
,求⊙O的半径r及sinB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com