
【题目】如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF. 
(1)求证:AB是⊙O的切线;
(2)若CF=4,DF= ![]() ,求⊙O的半径r及sinB.
,求⊙O的半径r及sinB.
【答案】
(1)证明:连接OA、OD,如图,
∵点D为CE的下半圆弧的中点,
∴OD⊥BC,
∴∠EOD=90°,
∵AB=BF,OA=OD,
∴∠BAF=∠BFA,∠OAD=∠D,
而∠BFA=∠OFD,
∴∠OAD+∠BAF=∠D+∠BFA=90°,即∠OAB=90°,
∴OA⊥AB,
∴AB是⊙O切线
(2)解:OF=CF﹣OC=4﹣r,OD=r,DF= ![]() ,
,
在Rt△DOF中,OD2+OF2=DF2,即r2+(4﹣r)2=( ![]() )2,
)2,
解得r1=3,r2=1(舍去);
∴半径r=3,
∴OA=3,OF=CF﹣OC=4﹣3=1,BO=BF+FO=AB+1.
在Rt△AOB中,AB2+OA2=OB2,
∴AB2+32=(AB+1)2,
∴AB=4,OB=5,
∴sinB= ![]() =
= ![]() .
.

【解析】(1)连接OA、OD,如图,根据垂径定理得OD⊥BC,则∠D+∠OFD=90°,再由AB=BF,OA=OD得到∠BAF=∠BFA,∠OAD=∠D,加上∠BFA=∠OFD,所以∠OAD+∠BAF=90°,则OA⊥AB,然后根据切线的判定定理即可得到AB是⊙O切线;(2)先表示出OF=4﹣r,OD=r,在Rt△DOF中利用勾股定理得r2+(4﹣r)2=( ![]() )2 , 解方程得到r的值,那么OA=3,OF=CF﹣OC=4﹣3=1,BO=BF+FO=AB+1. 然后在Rt△AOB中利用勾股定理得AB2+OA2=OB2 , 即AB2+32=(AB+1)2 , 解方程得到AB=4的值,再根据三角函数定义求出sinB.
)2 , 解方程得到r的值,那么OA=3,OF=CF﹣OC=4﹣3=1,BO=BF+FO=AB+1. 然后在Rt△AOB中利用勾股定理得AB2+OA2=OB2 , 即AB2+32=(AB+1)2 , 解方程得到AB=4的值,再根据三角函数定义求出sinB.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
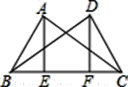
【题目】如图所示,△ABC和△DCB有公共边BC,且AB=DC,作AE⊥BC,DF⊥BC,垂足分别为E、F,AE=DF,那么求证AC=BD时,需要证明三角形全等的是Rt△ABE≌Rt△DCF,△AEC≌DFB.说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C、D均在以BC为直径的圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10,则图中阴影部分的面积为 . 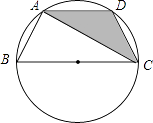
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,转盘上1、2、3、4四个数字分别代表鸡、猴、鼠、羊四种生肖邮票(每种邮票各两枚,鸡年邮票面值“80分”,其它邮票都是面值“1.20元”),转动转盘后,指针每落在某个数字所在扇形一次就表示获得该种邮票一枚. 
(1)任意转动转盘一次,获得猴年邮票的概率是;
(2)任意转动转盘两次,求获得的两枚邮票可以邮寄一封需2.4元邮资的信件的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )

A. BD=CE B. AD=AE C. DA=DE D. BE=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张在自家土地上平整出了一块苗圃,并将这块苗圃分成了四个长方形区域,其尺寸如图所示(图中长度单位:米),小张计划在这四个区域上按图中所示分别种植草本花卉 1 号、2 号、3 号、4 号.
(1)用式子表示这块苗圃的总面积;
(2)已知种植草本花卉 1 号、2 号、3 号、4 号的成本分别是每平方米 4 元、6 元、8 元、10 元.
①用式子表示小张在这块苗圃上种植草本花卉的总成本;
②当 a=9 时,求小张在这块苗圃上种植草本花卉的总成本.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线EF与MN相交于点O,∠MOE=30°,将一直角三角尺的直角顶点与点O重合,直角边OA与MN重合,OB在∠NOE内部.操作:将三角尺绕点O以每秒5°的速度沿顺时针方向旋转一周,设运动时间为t(s).
(1)当t为何值时,直角边OB恰好平分∠NOE?此时OA是否平分∠MOE?请说明理由;
(2)若在三角尺转动的同时,直线EF也绕点O以每秒8°的速度顺时针方向旋转一周,当一方先完成旋转一周时,另一方同时停止转动.
①当t为何值时,OE平分∠AOB?
②OE能否平分∠NOB?若能请直接写出t的值;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某商场有一双向运行的自动扶梯,扶梯上行和下行的速度保持不变且相同,甲、乙两人同时站上了此扶梯的上行和下行端,甲站上上行扶梯的同时又以0.8m/s的速度往上跑,乙站上下行扶梯后则站立不动随扶梯下行,两人在途中相遇,甲到达扶梯顶端后立即乘坐下行扶梯,同时以0.8m/s的速度往下跑,而乙到达底端后则在原地等候甲.图2中线段OB、AB分别表示甲、乙两人在乘坐扶梯过程中,离扶梯底端的路程y(m)与所用时间x(s)之间的部分函数关系,结合图象解答下列问题: 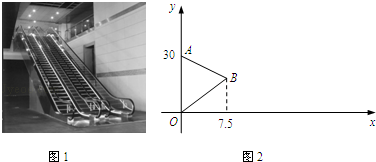
(1)点B的坐标是;
(2)求AB所在直线的函数关系式;
(3)乙到达扶梯底端后,还需等待多长时间,甲才到达扶梯底端?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com