
【题目】如图1,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.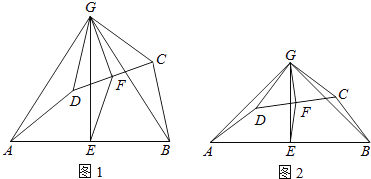
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2,若AD、BC所在直线互相垂直,求 ![]() 的值.
的值.
【答案】
(1)证明:∵GE是AB的垂直平分线,
∴GA=GB,
同理:GD=GC,
在△AGD和△BGC中,
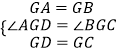 ,
,
∴△AGD≌△BGC(SAS),
∴AD=BC;
(2)证明:∵∠AGD=∠BGC,
∴∠AGB=∠DGC,
在△AGB和△DGC中, ![]() ,
,
∴△AGB∽△DGC,
∴ ![]() ,
,
又∵∠AGE=∠DGF,
∴∠AGD=∠EGF,
∴△AGD∽△EGF
(3)解:延长AD交GB于点M,交BC的延长线于点H,如图所示: 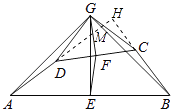
则AH⊥BH,
∵△AGD≌△BGC,
∴∠GAD=∠GBC,
在△GAM和△HBM中,∠GAD=∠GBC,∠GMA=∠HMB,
∴∠AGB=∠AHB=90°,
∴∠AGE= ![]() ∠AGB=45°,
∠AGB=45°,
∴ ![]() ,
,
又∵△AGD∽△EGF,
∴ ![]() =
= ![]() =
= ![]() .
.
【解析】(1)由GE是AB的垂直平分线,得到GA=GB,同理GD=GC,△AGD≌△BGC(SAS),得到AD=BC;(2)由∠AGD=∠BGC,得到∠AGB=∠DGC,在△AGB和△DGC中,由比值得到△AGB∽△DGC,得到EG:FG=GA:GD,又∠AGE=∠DGF,得到∠AGD=∠EGF,所以△AGD∽△EGF;(3)由△AGD≌△BGC,得到∠GAD=∠GBC,在△GAM和△HBM中,∠GAD=∠GBC,∠GMA=∠HMB,得到∠AGB=∠AHB=90°,∠AGE= ![]() ∠AGB=45°,又△AGD∽△EGF,得到
∠AGB=45°,又△AGD∽△EGF,得到![]() .
.
【考点精析】根据题目的已知条件,利用相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具商店销售功能相同的A、B两种品牌的计算器,购买2个A品牌和3个B品牌的计算器共需156元;购买3个A品牌和1个B品牌的计算器共需122元.
(1)求这两种品牌计算器的单价;
(2)学校开学前夕,该商店对这两种计算器开展了促销活动,具体办法如下:A品牌计算器按原价的八折销售,B品牌计算器超出5个的部分按原价的七折销售,设购买x个A品牌的计算器需要y1元,购买x(x>5)个B品牌的计算器需要y2元,分别求出y1、y2关于x的函数关系式;
(3)当需要购买50个计算器时,买哪种品牌的计算器更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,以BC边为直径作⊙O交AB边于点D,过点D作DE⊥AC于点E.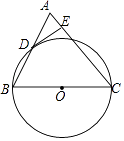
(1)求证:DE是⊙O的切线;
(2)若⊙O的半径等于 ![]() ,cosB=
,cosB= ![]() ,求线段DE的长.
,求线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对非负实数x“四舍五入”到个位的值记为(x).即当n为非负整数时,若![]() ,则(x)=n.如(0.46)=0,(3.67)=4.
,则(x)=n.如(0.46)=0,(3.67)=4.
给出下列关于(x)的结论:
①(1.493)=1;
②(2x)=2(x);
③若(![]() )=4,则实数x的取值范围是9≤x<11;
)=4,则实数x的取值范围是9≤x<11;
④当x≥0,m为非负整数时,有(m+2019x)=m+(2019x);
⑤(x+y)=(x)+(y);
其中,正确的结论有__________(填写所有正确的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,P为AD边上一点,沿直线BP将△ABP翻折至△EBP(点A的对应点为点E),PE与CD相交于点O,且OE=OD.
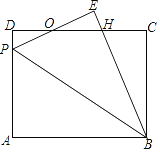
(1)求证:PE=DH;
(2)若AB=10,BC=8,求DP的长.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1) 先证明△DOP≌△EOH,再利用等量代换得到PE=DH.
(2) 设DP=x, Rt△BCH中,先用 x表示三角形三边,利用勾股定理列式解方程.
试题解析:
(1)解:证明:∵OD=OE,∠D=∠E=90°,∠DOP=∠EOH,
∴△DOP≌△EOH,
∴OP=OH,
∴PO+OE=OH+OD,
∴PE=DH.
(2)解:设DP=x,则EH=x,BH=10﹣x,
CH=CD﹣DH=CD﹣PE=10﹣(8﹣x)=2+x,
∴在Rt△BCH中,BC2+CH2=BH2
(2+x)2+82=(10﹣x)2,
∴x=![]() ,
,
∴DP=![]() .
.
【题型】解答题
【结束】
25
【题目】某文教店老板到批发市场选购A,B两种品牌的绘图工具套装,每套A品牌套装进价比B品牌每套套装进价多2.5元,已知用200元购进A种套装的数量是用75元购进B种套装数量的2倍.
(1)求A,B两种品牌套装每套进价分别为多少元?
(2)若A品牌套装每套售价为13元,B品牌套装每套售价为9.5元,店老板决定,购进B品牌的数量比购进A品牌的数量的2倍还多4套,两种工具套装全部售出后,要使总的获利超过120元,则最少购进A品牌工具套装多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.

(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,BC边上有一点E,BE=4,将纸片折叠,使A点与E点重合,折痕MN交AD于M点,则线段AM的长是_____.
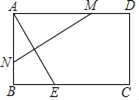
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com