
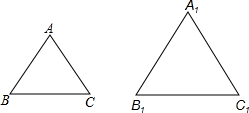
 如图,在等腰△ABC和等腰△A1B1C1中,底边的长BC=4cm,B1C1=6cm,它们的周长分别为16cm和24cm,那么这两个等腰三角形的腰与底边是否成比例线段,说明理由.
如图,在等腰△ABC和等腰△A1B1C1中,底边的长BC=4cm,B1C1=6cm,它们的周长分别为16cm和24cm,那么这两个等腰三角形的腰与底边是否成比例线段,说明理由. 分析 根据三角形的周长得到AB=$\frac{1}{2}$(16-4)=6,A1B1=$\frac{1}{2}$(24-6)=9,由于$\frac{AB}{{A}_{1}{B}_{1}}$=$\frac{6}{9}$=$\frac{2}{3}$,$\frac{BC}{{B}_{1}{C}_{1}}$=$\frac{4}{6}$=$\frac{2}{3}$,于是得到$\frac{AB}{{A}_{1}{B}_{1}}$=$\frac{BC}{{B}_{1}{C}_{1}}$,即可得到结论.
解答 解:这两个等腰三角形的腰与底边是成比例线段,
理由:∵在等腰△ABC和等腰△A1B1C1中,底边的长BC=4cm,B1C1=6cm,它们的周长分别为16cm和24cm,
∴AB=$\frac{1}{2}$(16-4)=6,A1B1=$\frac{1}{2}$(24-6)=9,
∵$\frac{AB}{{A}_{1}{B}_{1}}$=$\frac{6}{9}$=$\frac{2}{3}$,$\frac{BC}{{B}_{1}{C}_{1}}$=$\frac{4}{6}$=$\frac{2}{3}$,
∴$\frac{AB}{{A}_{1}{B}_{1}}$=$\frac{BC}{{B}_{1}{C}_{1}}$,
∴这两个等腰三角形的腰与底边是成比例线段.
点评 本题考查了比例线段,等腰三角形的性质,正确理解成比例线段的概念是解题的关键.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:初中数学 来源: 题型:解答题
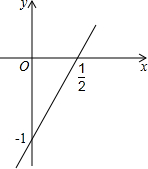 已知函数y=2x-1的图象如图所示,请根据图象回答下列问题:
已知函数y=2x-1的图象如图所示,请根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com