
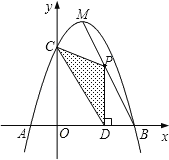
【题目】如图,已知关于x的二次函数y=﹣x2+bx+c(c>0)的图象与x轴相交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=OC=3,顶点为M.
(1)求出二次函数的关系式;
(2)点P为线段MB上的一个动点,过点P作x轴的垂线PD,垂足为D.若OD=m,△PCD的面积为S,求S关于m的函数关系式,并写出m的取值范围;
(3)探索线段MB上是否存在点P,使得△PCD为直角三角形?如果存在,求出P的坐标;如果不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,(
;(3)存在,(![]() ,3),(3
,3),(3![]() ﹣3,12﹣6
﹣3,12﹣6![]() )
)
【解析】
(1)根据题意得出点B和点C的坐标,将两点坐标代入即可得出函数解析式;
(2)根据(1)中函数解析式得出点M的坐标,根据OD=m设出点P的坐标,从而得出PD的长度,再根据![]() 得出S关于m的函数解析式;再根据点P在线段MB上得出m的取值范围;
得出S关于m的函数解析式;再根据点P在线段MB上得出m的取值范围;
(3)分别讨论∠PDC、∠DPC和∠DCP分别是直角的的情况是否存在,如果存在,根据实际情况,利用数形结合的思想得出点P的坐标.
解:(1)∵OB=OC=3,
∴B(3,0),C(0,3)
∴![]() ,
,
解得 ![]()
∴二次函数的解析式为![]() ;
;
(2)由(1)可得函数解析式为:![]() ,
,
∴M(1,4)
设直线MB的解析式为y=kx+n,将点M(1,4),点B(3,0)代入可得:
则有![]() ,
,
解得:![]() ,
,
∴直线MB的解析式为![]() ;
;
∵PD⊥x轴,OD=m,
∴点P的坐标为(m,![]() )
)
∴![]() ;
;
又∵点P为线段MB上的一个动点,且当点P与点B重合时,点P和点D重合,PCD不能构成三角形,
∴![]() ;
;
∴![]() ;
;
(3)∵若∠PDC是直角,则点C在x轴上,由函数图象可知点C在y轴的正半轴上,
∴∠PDC≠90°,
如图,在△PCD中,当∠DPC=90°时,
当CP![]() AB时,
AB时,
∵PD⊥AB,
∴CP⊥PD,
∴PD=OC=3,
∴P点纵坐标为:3,代入![]() ,
,
得:![]() ,此时
,此时![]() .
.
∴线段BM上存在点![]() 使△PCD为直角三角形.
使△PCD为直角三角形.
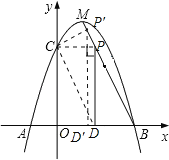
如图,当![]() 时,△COD′∽△D′CP′,
时,△COD′∽△D′CP′,
此时CD′2=COP′D′,
即![]() ,
,
∴![]()
解得:![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴P′![]()
综上所述:P点坐标为:(![]() ,3),
,3),![]() .
.


科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() (k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.
(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.
(1)求这个反比函数的表达式;
(2)求△ACD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受“新冠”疫情影响,全国中小学延迟开学,很多学校都开展起了“线上教学”,市场上对手写板的需求激增.重庆某厂家准备3月份紧急生产A,B两种型号的手写板,若生产20个A型号和30个B型号手写板,共需要投入36000元;若生产30个A型号和20个B型号手写板,共需要投入34000元.
(1)请问生产A,B两种型号手写板,每个各需要投入多少元的成本?
(2)经测算,生产的A型号手写板每个可获利200元,B型号手写板每个可获利400元,该厂家准备用10万元资金全部生产这两种手写板,总获利w元,设生产了A型号手写板a个,求w关于a的函数关系式;
查看答案和解析>>
科目:初中数学 来源: 题型:
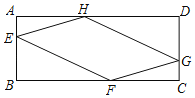
【题目】如图,点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA(不包括端点)上运动,且满足![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)试判断四边形EFGH的形状,并说明理由.
(3)请探究四边形EFGH的周长一半与矩形ABCD一条对角线长的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
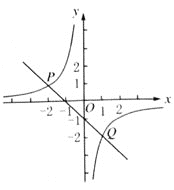
【题目】已知一次函数与反比例函数的图象交于点P(-2,1)和Q(1,m).
(1)求反比例函数的关系式;
(2)求Q点的坐标和一次函数的解析式;
(3)观察图象回答:当x为何值时,一次函数的值大于反比例函数的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
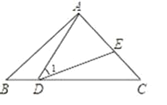
【题目】如图,点D,E分别在△ABC的边BC,AC上,连接AD,DE.
(1)若∠C=∠BAD,AB=5,求BD·BC的值;
(2)若点E是AC的中点,AD=![]() AE, 求证:∠1=∠C.
AE, 求证:∠1=∠C.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学计划购进若干个甲种规格的排球和乙种规格的足球. 如果购买20个甲种规格的排球和15个乙种规格的足球,一共需要花费2050元; 如果购买10个甲种规格的排球和20个乙种规格的足球,一共需要花费1900元.
(1)求每个甲种规格的排球和每个乙种规格的足球的价格分别是多少元?
(2)如果学校要购买甲种规格的排球和乙种规格的足球共50个,并且预算总费用不超过3210元,那么该学校至多能购买多少个乙种规格的足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某小区居民使用共享单车次数的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数统计如下:
使用次数 | 0 | 5 | 10 | 15 | 20 |
人数 | 1 | 1 | 4 | 3 | 1 |
(1)这10位居民一周内使用共享单车次数的中位数是 次,众数是 次.
(2)若小明同学把数据“20”看成了“30”,那么中位数,众数和平均数中不受影响的是 .(填“中位数”,“众数”或“平均数”)
(3)若该小区有2000名居民,试估计该小区居民一周内使用共享单车的总次数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com