
【题目】受“新冠”疫情影响,全国中小学延迟开学,很多学校都开展起了“线上教学”,市场上对手写板的需求激增.重庆某厂家准备3月份紧急生产A,B两种型号的手写板,若生产20个A型号和30个B型号手写板,共需要投入36000元;若生产30个A型号和20个B型号手写板,共需要投入34000元.
(1)请问生产A,B两种型号手写板,每个各需要投入多少元的成本?
(2)经测算,生产的A型号手写板每个可获利200元,B型号手写板每个可获利400元,该厂家准备用10万元资金全部生产这两种手写板,总获利w元,设生产了A型号手写板a个,求w关于a的函数关系式;
【答案】(1)生产A种型号的手写板需要投入成本600元,生产B种型号的手写板需要投入成本800元;(2)![]()
【解析】
(1)根据生产20个A型号和30个B型号手写板,共需要投入36000元;若生产30个A型号和20个B型号手写板,共需要投入34000元,可以列出相应的二元一次方程组,从而可以求得生产A,B两种型号手写板,每个各需要投入多少元的成本;
(2)根据题意和(1)中的结果可以得到w与a的函数关系式.
解:(1)设生产A种型号的手写板需要投入成本a元,生产B种型号的手写板需要投入成本b元,
由题意可得![]()
解得![]() ,
,
答:生产A种型号的手写板需要投入成本600元,生产B种型号的手写板需要投入成本800元;
(2)∵该厂家准备用10万元资金全部生产这两种手写板,生产了A型号手写板a个,
∴生产B型号的手写板的数量为:![]() (个),
(个),
![]() ,
,
即w关于a的函数关系式为![]() .
.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】关于x的二次函数y=x2+2kx+k﹣1,下列说法正确的是( )
A.对任意实数k,函数图象与x轴都没有交点
B.对任意实数k,函数图象没有唯一的定点
C.对任意实数k,函数图象的顶点在抛物线y=﹣x2﹣x﹣1上运动
D.对任意实数k,当x≥﹣k﹣1时,函数y的值都随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】投资1万元围一个矩形菜园(如图),其中一边靠墙,另外三边选用不同材料建造.墙长24 m,平行于墙的边的费用为200元/m,垂直于墙的边的费用为150元/m,设平行于墙的边长为x m.
(1)设垂直于墙的一边长为y m,直接写出y与x之间的函数关系式;
(2)若菜园面积为384 m2,求x的值;
(3)求菜园的最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD的两条对角线AC、BD互相平分.添加下列条件,一定能判定四边形ABCD为菱形的是( )
A.∠ABD=∠BDCB.∠ABD=∠BACC.∠ABD=∠CBDD.∠ABD=∠BCA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知半圆⊙O的直径AB=10,弦CD∥AB,且CD=8,E为弧CD的中点,点P在弦CD上,联结PE,过点E作PE的垂线交弦CD于点G,交射线OB于点F.
(1)当点F与点B重合时,求CP的长;
(2)设CP=x,OF=y,求y与x的函数关系式及定义域;
(3)如果GP=GF,求△EPF的面积.
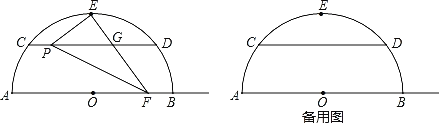
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
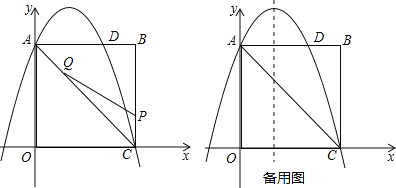
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
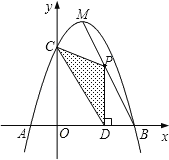
【题目】如图,已知关于x的二次函数y=﹣x2+bx+c(c>0)的图象与x轴相交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=OC=3,顶点为M.
(1)求出二次函数的关系式;
(2)点P为线段MB上的一个动点,过点P作x轴的垂线PD,垂足为D.若OD=m,△PCD的面积为S,求S关于m的函数关系式,并写出m的取值范围;
(3)探索线段MB上是否存在点P,使得△PCD为直角三角形?如果存在,求出P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,且点
,且点![]() 与点
与点![]() 的坐标分别为
的坐标分别为![]() .
.![]() ,点
,点![]() 是抛物线的顶点.点
是抛物线的顶点.点![]() 为线段
为线段![]() 上一个动点,过点
上一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,若
,若![]() .
.
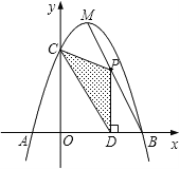
(1)求二次函数解析式;
(2)设![]() 的面积为
的面积为![]() ,试判断
,试判断![]() 有最大值或最小值?若有,求出其最值,若没有,请说明理由;
有最大值或最小值?若有,求出其最值,若没有,请说明理由;
(3)在![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为直角三角形?若存在,请写出点
为直角三角形?若存在,请写出点![]() 的坐标若不存在,请说明理由.
的坐标若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com