
【题目】关于x的二次函数y=x2+2kx+k﹣1,下列说法正确的是( )
A.对任意实数k,函数图象与x轴都没有交点
B.对任意实数k,函数图象没有唯一的定点
C.对任意实数k,函数图象的顶点在抛物线y=﹣x2﹣x﹣1上运动
D.对任意实数k,当x≥﹣k﹣1时,函数y的值都随x的增大而增大
 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
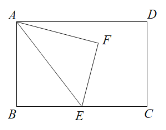
【题目】如图,在矩形ABCD中,AB=10,BC=m,E为BC边上一点,沿AE翻折△ABE,点B落在点F处.
(1)连接CF,若CF//AE,求EC的长(用含m的代数式表示);
(2)若EC=![]() ,当点F落在矩形ABCD的边上时,求m的值;
,当点F落在矩形ABCD的边上时,求m的值;
(3)连接DF,在BC边上是否存在两个不同位置的点E,使得?若存![]() 在,直接写出m的取值范围;若不存在,说明理由.
在,直接写出m的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
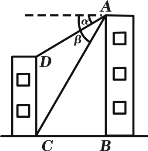
【题目】如图,从甲楼顶部A处测得乙楼顶部D处的俯角α为30°,又从A处测得乙楼底部C处的俯角β为60°.已知两楼之间的距离BC为18米,则乙楼CD的高度为__________.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
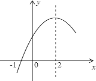
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(-3,y1)、点B(-![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2.其中正确的结论有( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:有一内角为直角的三角形叫做直角三角形.类似地我们定义:有一内角为45°的三角形叫做半直角三角形.如图,在平面直角坐标系中,O为原点,A(2,0),B(-2,0),D是y轴上的一个动点,∠ADC=90°(A、D、C按顺时针方向排列), BC与经过A、B、D三点的⊙M交于点E,DE平分∠ADC,连结AE,BD.显然ΔDCE、ΔDEF、ΔDAE是半直角三角形.
(1)求证:ΔABC是半直角三角形;
(2)求证:∠DEC=∠DEA;
(3)若点D的坐标为(0,8),求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
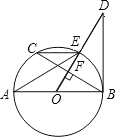
【题目】已知:如图,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,若∠AEC=∠ODB.
(1)求证:BD是⊙O的切线;
(2)当AB=10,BC=8时,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
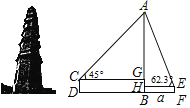
【题目】慈氏塔位于岳阳市城西洞庭湖边,是湖南省保存最好的古塔建筑之一.如图,小亮的目高CD为1.7米,他站在D处测得塔顶的仰角∠ACG为45°,小琴的目高EF为1.5米,她站在距离塔底中心B点a米远的F处,测得塔顶的仰角∠AEH为62.3°.(点D、B、F在同一水平线上,参考数据:sin62.3°≈0.89,cos62.3°≈0.46,tan62.3°≈1.9)
(1)求小亮与塔底中心的距离BD;(用含a的式子表示)
(2)若小亮与小琴相距52米,求慈氏塔的高度AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() (k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.
(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.
(1)求这个反比函数的表达式;
(2)求△ACD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受“新冠”疫情影响,全国中小学延迟开学,很多学校都开展起了“线上教学”,市场上对手写板的需求激增.重庆某厂家准备3月份紧急生产A,B两种型号的手写板,若生产20个A型号和30个B型号手写板,共需要投入36000元;若生产30个A型号和20个B型号手写板,共需要投入34000元.
(1)请问生产A,B两种型号手写板,每个各需要投入多少元的成本?
(2)经测算,生产的A型号手写板每个可获利200元,B型号手写板每个可获利400元,该厂家准备用10万元资金全部生产这两种手写板,总获利w元,设生产了A型号手写板a个,求w关于a的函数关系式;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com