
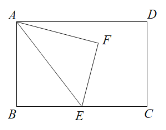
【题目】如图,在矩形ABCD中,AB=10,BC=m,E为BC边上一点,沿AE翻折△ABE,点B落在点F处.
(1)连接CF,若CF//AE,求EC的长(用含m的代数式表示);
(2)若EC=![]() ,当点F落在矩形ABCD的边上时,求m的值;
,当点F落在矩形ABCD的边上时,求m的值;
(3)连接DF,在BC边上是否存在两个不同位置的点E,使得?若存![]() 在,直接写出m的取值范围;若不存在,说明理由.
在,直接写出m的取值范围;若不存在,说明理由.
【答案】(1)EC=![]() ;(2)
;(2)![]() 或
或![]() ;(3)存在,
;(3)存在,![]()
【解析】
(1)由翻折的性质可知BF⊥AE,CF//AE,所以![]() ,根据直角三角形的性质,两锐角互余,可证得EF=EC,所以点E是BC的中点,即可求得EC的长;
,根据直角三角形的性质,两锐角互余,可证得EF=EC,所以点E是BC的中点,即可求得EC的长;
(2)分两种情况进行分类讨论,当点F在AD边上,很容易可证得四边形ABEF是正方形,所以BE=![]() ,就可求出m的值,当点F在CD上,由翻折的性质可得,
,就可求出m的值,当点F在CD上,由翻折的性质可得,![]() ,AB=AF=10,在△ECF中由勾股定理可表示出CF的长,在△ADF中,由勾股定理即可求出m的值;
,AB=AF=10,在△ECF中由勾股定理可表示出CF的长,在△ADF中,由勾股定理即可求出m的值;
(3)由![]() 可知,点F到AD边的距离为5,有两种情况,第一种情况当点F在矩形内,可得
可知,点F到AD边的距离为5,有两种情况,第一种情况当点F在矩形内,可得![]() ,第二种情况当点F在AD边上方,可得
,第二种情况当点F在AD边上方,可得![]() ,要使在BC边上存在两个不同位置的点E,所以
,要使在BC边上存在两个不同位置的点E,所以![]() .
.
(1)连接CF,BF,BF交AE于点H,如下图所示:

∵△ABE沿AE翻折到了△AFE,由翻折可得:
∴BE=EF,BF⊥AE,
∴![]() ,
,
∵CF//AE,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵BE=EF
∴∠BFE=∠FBE
∴∠EFC=∠ECF
∴EF=EC
∴EC=![]() .
.
(2)①当点F在AD上,如下图所示:
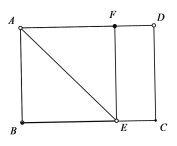
由翻折可得:
AB=AF=10,BE=EF,∠BAE=∠FAE=45![]()
∵四边形ABCD是矩形,
∴∠ABE=90![]() ,AD//BC,
,AD//BC,
∴△ABE是等腰直角三角形,
∴AB=BE=AF=10,
∴四边形ABEF是正方形,
∵EC=![]() ,
,
∴![]() =10
=10
∴![]() ;
;
②当点F在边CD上,如下图所示:

∵EC=![]() ,
,
∴![]()
由翻折可得:
BE=EF,AB=AF=10,
在Rt△ECF中,由勾股定理得:
![]()
∴![]() ,
,
在Rt△ADF中,由勾股定理得:
![]() ,
,
解得:![]()
∴综上所述:![]() 或
或![]() .
.
(3)存在,
过F点作AD的垂线,交AD于G点,设FG为h,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
①当点F再AD的下方,点E和点C重合时,如图所示:

在△AGF中,由勾股定理得:
![]() ,
,
∴![]() ,
,
在△EHF中,由勾股定理得:
![]() ,
,
![]() ,
,
当点F在AD的上方时,点E和点C重合,如图所示:
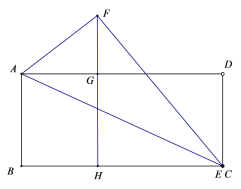
在△AGF中,由勾股定理得:
![]() ,
,
∴![]() ,
,
在△EHF中,由勾股定理得:
![]() ,
,
![]() ,
,
∴在BC边上存在两个不同位置的点E,![]() ,
,
故答案为:![]() .
.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】(抗击疫情)为了遏制新型冠状病毒疫情的蔓延势头,各地教育部门在推迟各级学校开学时间的同时提出“听课不停学”的要求,各地学校也都开展了远程网络教学,某校集中为学生提供四类在线学习方式:在线阅读、在线听课、在线答疑、在线讨论,为了了解学生的需求,该校通过网络对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据结果绘制成如下两幅不完整的统计图。

(1)本次调查的人数有多少人?
(2)请补全条形图;
(3)请求出“在线答疑”在扇形图中的圆心角度数;
(4)小宁和小娟都参加了远程网络教学活动,请求出小宁和小娟选择同一种学习方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1,E1,E2,C2,E3,E4,C3……在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3……,则正方形A2020B2020C2020D2020的边长是( )
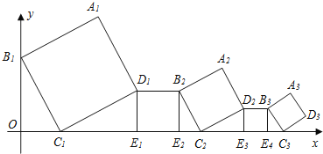
A.(![]() )2017B.(
)2017B.(![]() )2018C.(
)2018C.(![]() )2019D.(
)2019D.(![]() )2020
)2020
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一条直线把一个四边形分成两部分,这两部分图形的周长相等,那么这条直线称为这个四边形的“等分周长线”.在直角梯形ABCD中,AB∥CD,∠A=90°,DC=AD,∠B是锐角,cotB=![]() ,AB=17.如果点E在梯形的边上,CE是梯形ABCD的“等分周长线”,那么△BCE的周长为____.
,AB=17.如果点E在梯形的边上,CE是梯形ABCD的“等分周长线”,那么△BCE的周长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个少年在绿茵场上游戏.小红从点A出发沿线段AB运动到点B,小兰从点C出发,以相同的速度沿⊙O逆时针运动一周回到点C,两人的运动路线如图1所示,其中AC=DB.两人同时开始运动,直到都停止运动时游戏结束,其间他们与点C的距离y与时间x(单位:秒)的对应关系如图2所示.则下列说法正确的有________.(填序号)
①小红的运动路程比小兰的长;② 两人分别在1.09秒和7.49秒的时刻相遇;③ 当小红运动到点D的时候,小兰已经经过了点D ;④在4.84秒时,两人的距离正好等于⊙O的半径.
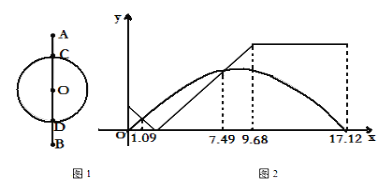
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根,且其中一个根是另一个根的2倍,则称这样的方程为“倍根方程”.现有下列结论: ①方程x2+2x﹣8=0是倍根方程;
②若关于x的方程x2+ax+2=0是倍根方程,则a=±3;
③若关于x的方程ax2﹣6ax+c=0(a≠0)是倍根方程,则抛物线y=ax2﹣6ax+c与x轴的公共点的坐标是(2,0)和(4,0);
④若点(m,n)在反比例函数y=![]() 的图象上,则关于x的方程mx2+5x+n=0是倍根方程.
的图象上,则关于x的方程mx2+5x+n=0是倍根方程.
上述结论中正确的有( )
A. ①② B. ③④ C. ②③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图示,AB是⊙O的直径,点F是半圆上的一动点(F不与A,B重合),弦AD平分∠BAF,过点D作DE⊥AF交射线AF于点AF.
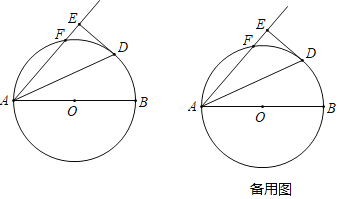
(1)求证:DE与⊙O相切:
(2)若AE=8,AB=10,求DE长;
(3)若AB=10,AF长记为x,EF长记为y,求y与x之间的函数关系式,并求出AFEF的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的二次函数y=x2+2kx+k﹣1,下列说法正确的是( )
A.对任意实数k,函数图象与x轴都没有交点
B.对任意实数k,函数图象没有唯一的定点
C.对任意实数k,函数图象的顶点在抛物线y=﹣x2﹣x﹣1上运动
D.对任意实数k,当x≥﹣k﹣1时,函数y的值都随x的增大而增大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com