
ЁОЬтФПЁПЃЈПЙЛївпЧщЃЉЮЊСЫЖєжЦаТаЭЙкзДВЁЖОвпЧщЕФТћбгЪЦЭЗЃЌИїЕиНЬг§ВПУХдкЭЦГйИїМЖбЇаЃПЊбЇЪБМфЕФЭЌЪБЬсГіЁАЬ§ПЮВЛЭЃбЇЁБЕФвЊЧѓЃЌИїЕибЇаЃвВЖМПЊеЙСЫдЖГЬЭјТчНЬбЇЃЌФГаЃМЏжаЮЊбЇЩњЬсЙЉЫФРрдкЯпбЇЯАЗНЪНЃКдкЯпдФЖСЁЂдкЯпЬ§ПЮЁЂдкЯпД№вЩЁЂдкЯпЬжТлЃЌЮЊСЫСЫНтбЇЩњЕФашЧѓЃЌИУаЃЭЈЙ§ЭјТчЖдБОаЃВПЗжбЇЩњНјааСЫЁАФуЖдФФРрдкЯпбЇЯАЗНЪНзюИааЫШЄЁБЕФЕїВщЃЌВЂИљОнНсЙћЛцжЦГЩШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЁЃ

ЃЈ1ЃЉБОДЮЕїВщЕФШЫЪ§гаЖрЩйШЫЃП
ЃЈ2ЃЉЧыВЙШЋЬѕаЮЭМЃЛ
ЃЈ3ЃЉЧыЧѓГіЁАдкЯпД№вЩЁБдкЩШаЮЭМжаЕФдВаФНЧЖШЪ§ЃЛ
ЃЈ4ЃЉаЁФўКЭаЁОъЖМВЮМгСЫдЖГЬЭјТчНЬбЇЛюЖЏЃЌЧыЧѓГіаЁФўКЭаЁОъбЁдёЭЌвЛжжбЇЯАЗНЪНЕФИХТЪ.
ЁОД№АИЁПЃЈ1ЃЉ100ЃЛЃЈ2ЃЉВЙШЋЭМаЮМћНтЮіЃЛЃЈ3ЃЉ72ЁуЃЛЃЈ4ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОндкЯпдФЖСЕФШЫЪ§КЭАйЗжБШЃЌМДПЩЧѓГіЕїВщЕФШЫЪ§ЃЛ
ЃЈ2ЃЉРћгУЕїВщЕФзмШЫЪ§ЃЌЯШЧѓГідкЯпД№вЩЕФШЫЪ§ЃЌШЛКѓВЙШЋЬѕаЮЭММДПЩЃЛ
ЃЈ3ЃЉИљОндкЯпД№вЩЕФШЫЪ§ЃЌМДПЩЧѓГіЫќдкЩШаЮЭГМЦЭМжаЕФдВаФНЧЖШЪ§ЃЛ
ЃЈ4ЃЉРћгУЪїзДЭМЗЈЕУЕНЫљгаЕФПЩФмЃЌШЛКѓИљОнаЁФўКЭаЁОъбЁдёЭЌвЛжжбЇЯАЗНЪНЕФПЩФмЃЌРћгУИХТЪЙЋЪНЃЌМДПЩЧѓГіИХТЪ.
НтЃКЃЈ1ЃЉЬѕаЮЭГМЦЭМжаЁАдкЯпдФЖСЁБЕФШЫЪ§ЮЊ25ШЫЃЌ
ЩШаЮЭГМЦЭМжаЁАдкЯпдФЖСЁБЫљеМЕФБШР§ЮЊЃК![]() ЃЌ
ЃЌ
ЁрБОДЮЕїВщЕФзмШЫЪ§ЮЊЃК![]() ЃЈШЫЃЉЃЎ
ЃЈШЫЃЉЃЎ
ЃЈ2ЃЉЁпЁАдкЯпД№вЩЁБЕФШЫЪ§ЮЊЃК![]() ЃЈШЫЃЉЃЌ
ЃЈШЫЃЉЃЌ
ВЙЬѕаЮЭГМЦЭМШчЭМЃК

ЃЈ3ЃЉЁпЁАдкЯпД№вЩЁБЕФШЫЪ§ЮЊ20ШЫЃЌ
Ёр![]() ЃЛ
ЃЛ
Д№ЃКЩШаЮЭГМЦЭМжаЃЌЁАдкЯпД№вЩЁБЖдгІЕФЩШаЮдВаФНЧЕФЖШЪ§ЮЊ![]() ЃЛ
ЃЛ
ЃЈ4ЃЉМЧЫФжжбЇЯАЗНЪНЃКдкЯпдФЖСЁЂдкЯпЬ§ПЮЁЂдкЯпД№вЩЁЂдкЯпЬжТлЃЌЗжБ№ЮЊ![]() ЃЎ
ЃЎ
дђПЩЛЪїзДЭМШчЭМЫљЪОЃК
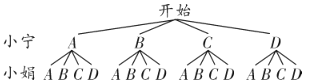
гЩЪїзДЭМПЩЕУЙВга16жжЕШПЩФмЕФЧщПіЃЌЦфжааЁФўКЭаЁОъбЁдёЭЌвЛжжбЇЯАЗНЪНЕФга4жжЧщПіЃЌ
ЁрPЃЈаЁФўКЭаЁОъбЁдёЭЌвЛжжбЇЯАЗНЪНЃЉ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
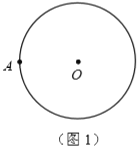
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЖдЁїABC НјаабЛЗЭљИДЕФжсЖдГЦЛђжааФЖдГЦБфЛЛЃЌШєдРДЕу A зјБъЪЧ(aЃЌb)ЃЌдђОЙ§Ек 2012 ДЮБфЛЛКѓЫљЕУЕФ A ЕузјБъЪЧ( )
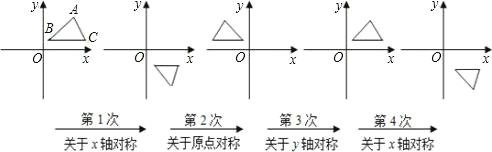
A. (aЃЌb) B. (aЃЌЉb) C. (ЉaЃЌb) D. (ЉaЃЌЉb)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮ![]() ЕФБпГЄЮЊ4ЃЌбгГЄ
ЕФБпГЄЮЊ4ЃЌбгГЄ![]() жС
жС![]() ЪЙ
ЪЙ![]() ЃЌвд
ЃЌвд![]() ЮЊБпдкЩЯЗНзїе§ЗНаЮ
ЮЊБпдкЩЯЗНзїе§ЗНаЮ![]() ЃЌбгГЄ
ЃЌбгГЄ![]() НЛ
НЛ![]() гк
гк![]() ЃЌСЌНг
ЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌСЌНг
ЕФжаЕуЃЌСЌНг![]() ЗжБ№гы
ЗжБ№гы![]() ЁЂ
ЁЂ![]() НЛгкЕу
НЛгкЕу![]() ЁЂ
ЁЂ![]() .дђЯТСаНсТлЃКЂй
.дђЯТСаНсТлЃКЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂм
ЃЛЂм![]() .Цфжае§ШЗЕФНсТлга( )
.Цфжае§ШЗЕФНсТлга( )

A. 1ИіB. 2ИіC. 3ИіD. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
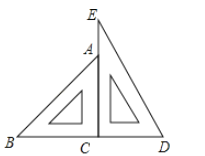
ЁОЬтФПЁПвЛИБШ§НЧГпАДШчЭМЕФЮЛжУАкЗХЃЈЖЅЕуC гыF жиКЯЃЌБпCAгыБпFEЕўКЯЃЌЖЅЕуBЁЂCЁЂDдквЛЬѕжБЯпЩЯЃЉЃЎНЋШ§НЧГпABCШЦзХЕуCАДФцЪБеыЗНЯђа§зЊnЁуКѓЃЈ0ЃМnЃМ360 ЃЉЃЌШєEDЁЭABЃЌдђnЕФжЕЪЧ_______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
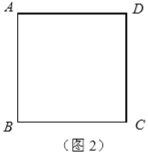
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЮЊе§ЗНаЮЃЌEЮЊЖдНЧЯпBDЩЯЕФЖЏЕуЃЌЙ§ЕуEзїFGЁЭAEЃЌFGНЛЩфЯпCDгкFЃЌНЛЩфЯпCBгкGЃЎ
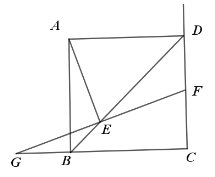
ЃЈ1ЃЉЧѓжЄЃКEF=EG
ЃЈ2ЃЉЧѓжЄЃК![]()
ЃЈ3ЃЉШєAB=4ЃЌЕБЁЯGEB=22.5ЁуЃЌжБНгаДГіCFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮ![]() ЮЊе§ЗНаЮЃЌ
ЮЊе§ЗНаЮЃЌ![]() ЮЊЖдНЧЯп
ЮЊЖдНЧЯп![]() ЩЯЕФЖЏЕуЃЌЙ§Еу
ЩЯЕФЖЏЕуЃЌЙ§Еу![]() зї
зї![]() ЃЌ
ЃЌ![]() НЛЩфЯп
НЛЩфЯп![]() гк
гк![]() ЃЌНЛЩфЯп
ЃЌНЛЩфЯп![]() гк
гк![]() ЃЎ
ЃЎ
(1)ЧѓжЄЃЛ![]() ЃЛ
ЃЛ
(2)ЧѓжЄЃЛ![]() ЃЛ
ЃЛ
(3)Шє![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌжБНгаДГі
ЪБЃЌжБНгаДГі![]() ЕФГЄЃЎ
ЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉШчЭМ1ЃЌЕу![]() дк
дк![]() ЩЯЃЌЧыдкЭМжагУжБГпЃЈВЛКЌПЬЖШЃЉКЭдВЙцзїЕШБпШ§НЧаЮ
ЩЯЃЌЧыдкЭМжагУжБГпЃЈВЛКЌПЬЖШЃЉКЭдВЙцзїЕШБпШ§НЧаЮ![]() ЃЌЪЙЕУЕу
ЃЌЪЙЕУЕу![]() ЁЂ
ЁЂ![]() ЖМдк
ЖМдк![]() ЩЯЃЎ
ЩЯЃЎ
ЃЈ2ЃЉвбжЊОиаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЂйШчЭМ2ЃЌЕБ![]() ЪБЃЌЧыдкЭМжагУжБГпЃЈВЛКЌПЬЖШЃЉКЭдВЙцзїЕШБпШ§НЧаЮ
ЪБЃЌЧыдкЭМжагУжБГпЃЈВЛКЌПЬЖШЃЉКЭдВЙцзїЕШБпШ§НЧаЮ![]() ЃЌЪЙЕУЕу
ЃЌЪЙЕУЕу![]() дкБп
дкБп![]() ЩЯЃЌЕу
ЩЯЃЌЕу![]() дкБп
дкБп![]() ЩЯЃЛ
ЩЯЃЛ
ЂкШєдкИУОиаЮжазмФмзїГіЗћКЯЂйжавЊЧѓЕФЕШБпШ§НЧаЮ![]() ЃЌЧыжБНгаДГі
ЃЌЧыжБНгаДГі![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
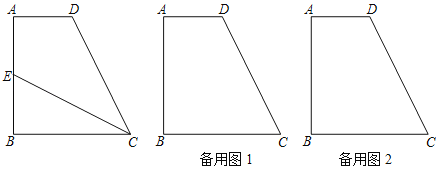
ЁОЬтФПЁПШчЭМЃЌвбжЊЬнаЮABCDжаЃЌADЁЮBCЃЌABЁЭBCЃЌADЃМBCЃЌABЃНBCЃН1ЃЌEЪЧБпABЩЯвЛЕуЃЌСЊНсCEЃЎ
ЃЈ1ЃЉШчЙћCEЃНCDЃЌЧѓжЄЃКADЃНAEЃЛ
ЃЈ2ЃЉСЊНсDEЃЌШчЙћДцдкЕуEЃЌЪЙЕУЁїADEЁЂЁїBCEКЭЁїCDEСНСНЯрЫЦЃЌЧѓADЕФГЄЃЛ
ЃЈ3ЃЉЩшЕуEЙигкжБЯпCDЕФЖдГЦЕуЮЊMЃЌЕуDЙигкжБЯпCEЕФЖдГЦЕуЮЊNЃЌШчЙћADЃН![]() ЃЌЧвMдкжБЯпADЩЯЪБЃЌЧѓ
ЃЌЧвMдкжБЯпADЩЯЪБЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
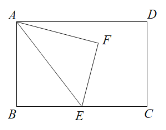
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌAB=10ЃЌBC=mЃЌEЮЊBCБпЩЯвЛЕуЃЌбиAEЗелЁїABEЃЌЕуBТфдкЕуFДІЃЎ
ЃЈ1ЃЉСЌНгCFЃЌШєCF//AEЃЌЧѓECЕФГЄЃЈгУКЌmЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ2ЃЉШєEC=![]() ЃЌЕБЕуFТфдкОиаЮABCDЕФБпЩЯЪБЃЌЧѓmЕФжЕЃЛ
ЃЌЕБЕуFТфдкОиаЮABCDЕФБпЩЯЪБЃЌЧѓmЕФжЕЃЛ
ЃЈ3ЃЉСЌНгDFЃЌдкBCБпЩЯЪЧЗёДцдкСНИіВЛЭЌЮЛжУЕФЕуEЃЌЪЙЕУЃПШєДц![]() дкЃЌжБНгаДГіmЕФШЁжЕЗЖЮЇЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
дкЃЌжБНгаДГіmЕФШЁжЕЗЖЮЇЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com