
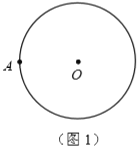
【题目】(1)如图1,点![]() 在
在![]() 上,请在图中用直尺(不含刻度)和圆规作等边三角形
上,请在图中用直尺(不含刻度)和圆规作等边三角形![]() ,使得点
,使得点![]() 、
、![]() 都在
都在![]() 上.
上.
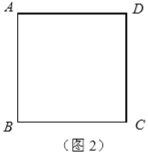
(2)已知矩形![]() 中,
中,![]() ,
,![]() .
.
①如图2,当![]() 时,请在图中用直尺(不含刻度)和圆规作等边三角形
时,请在图中用直尺(不含刻度)和圆规作等边三角形![]() ,使得点
,使得点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上;
上;
②若在该矩形中总能作出符合①中要求的等边三角形![]() ,请直接写出
,请直接写出![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)①见解析;②![]() 的取值范围是
的取值范围是![]() .
.
【解析】
解:(1) 作直径![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径作弧,交
为半径作弧,交![]() 于点
于点![]() 、
、![]() ,连
,连![]() 、
、![]() 、
、![]() 即可得到等边三角形
即可得到等边三角形![]() .
.
(2) ①连![]() ,在
,在![]() 上任取一点
上任取一点![]() ,以
,以![]() 为半径作
为半径作![]() ,交
,交![]() 于点
于点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径作弧,交
为半径作弧,交![]() 于点
于点![]() 、
、![]() ,连
,连![]() 、
、![]() 并延长,交
并延长,交![]() 、
、![]() 于点
于点![]() 、
、![]() ,连
,连![]() ,则
,则![]() 就是所要求作的.
就是所要求作的.
②分两种情况讨论,运用等边三角形的性质和勾股定理得到m的最大值和最小值即可;
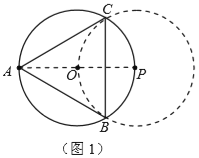
解:(1)如图1,作直径![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径作弧,交
为半径作弧,交![]() 于点
于点![]() 、
、![]() ,连
,连![]() 、
、![]() 、
、![]() ,则
,则![]() 就是所要求作的.
就是所要求作的.
(2)①如图2,连![]() ,在
,在![]() 上任取一点
上任取一点![]() ,以
,以![]() 为半径作
为半径作![]() ,交
,交![]() 于点
于点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径作弧,交
为半径作弧,交![]() 于点
于点![]() 、
、![]() ,连
,连![]() 、
、![]() 并延长,交
并延长,交![]() 、
、![]() 于点
于点![]() 、
、![]() ,连
,连![]() ,则
,则![]() 就是所要求作的.
就是所要求作的.
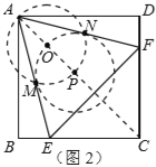
②一开始E点从B点出发,往C的方向运动,AF可以看成AE逆时针旋转60度得到,因此F是往上运动的,但是AE一直在变长,如果BC的长度不变的话,AF就是变少。(但是要保持AE=AF)只能变长BC了。所以E点从B点出发,往C的方向运动过程中,BC一直在变长。F最多只能到D点,因此F在D点处,BC就是最长了,因此得到如下的两个临界值:
如图,当E点与B点重合时,此时是临界点的最小值,
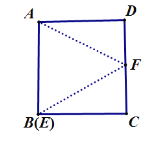
∵△AFE是等边三角形,
∴EF=AB=4,∠AEF=60°,
∴∠FEC=30°,
∴FC=2(直角三角形中30°所对的直角边等于斜边的一半),
∴此时![]() ,
,
当F点与D点重合时,此时是临界点的最大值,
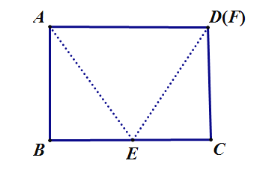
∵△AFE是等边三角形,
∴AD=AE,∠BAE=90°-60°=30°,
假设AD=AE=2x,
∴FC=x(直角三角形中30°所对的直角边等于斜边的一半),
∴此时![]() ,
,
解得![]() ,
,
∴![]() ,
,
∴![]() 的取值范围是
的取值范围是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
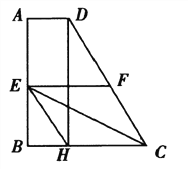
【题目】如图,在四边形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=6,CD=8,E,F分别是边ABCD的中点, DH⊥BC于点H,连接EH,EC,EF,现有下列结论:①∠CDH=30°;②EF=4;③四边形EFCH是菱形;④S△EFC=3S△BEH.你认为结论正确的有___________.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
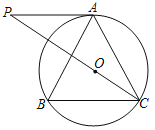
【题目】如图,△ABC内接于⊙O,AB=AC,过A作AP∥BC交CO的延长线于点P.
(1)求证:PA是⊙O的切线;
(2)若BC=8,tanB=2,求PA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(抗击疫情)为了遏制新型冠状病毒疫情的蔓延势头,各地教育部门在推迟各级学校开学时间的同时提出“听课不停学”的要求,各地学校也都开展了远程网络教学,某校集中为学生提供四类在线学习方式:在线阅读、在线听课、在线答疑、在线讨论,为了了解学生的需求,该校通过网络对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据结果绘制成如下两幅不完整的统计图。

(1)本次调查的人数有多少人?
(2)请补全条形图;
(3)请求出“在线答疑”在扇形图中的圆心角度数;
(4)小宁和小娟都参加了远程网络教学活动,请求出小宁和小娟选择同一种学习方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AC=2,AB=3,BC=4,点G是△ABC的重心.将△ABC平移,使得顶点A与点G重合.那么平移后的三角形与原三角形重叠部分的周长为( )
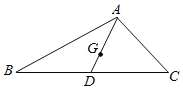
A.2B.3C.4D.4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1,E1,E2,C2,E3,E4,C3……在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3……,则正方形A2020B2020C2020D2020的边长是( )
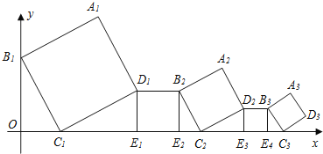
A.(![]() )2017B.(
)2017B.(![]() )2018C.(
)2018C.(![]() )2019D.(
)2019D.(![]() )2020
)2020
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根,且其中一个根是另一个根的2倍,则称这样的方程为“倍根方程”.现有下列结论: ①方程x2+2x﹣8=0是倍根方程;
②若关于x的方程x2+ax+2=0是倍根方程,则a=±3;
③若关于x的方程ax2﹣6ax+c=0(a≠0)是倍根方程,则抛物线y=ax2﹣6ax+c与x轴的公共点的坐标是(2,0)和(4,0);
④若点(m,n)在反比例函数y=![]() 的图象上,则关于x的方程mx2+5x+n=0是倍根方程.
的图象上,则关于x的方程mx2+5x+n=0是倍根方程.
上述结论中正确的有( )
A. ①② B. ③④ C. ②③ D. ②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com