
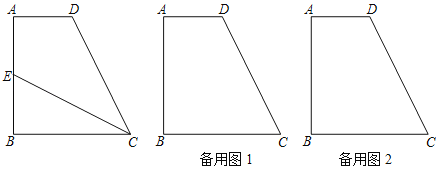
【题目】如图,已知梯形ABCD中,AD∥BC,AB⊥BC,AD<BC,AB=BC=1,E是边AB上一点,联结CE.
(1)如果CE=CD,求证:AD=AE;
(2)联结DE,如果存在点E,使得△ADE、△BCE和△CDE两两相似,求AD的长;
(3)设点E关于直线CD的对称点为M,点D关于直线CE的对称点为N,如果AD=![]() ,且M在直线AD上时,求
,且M在直线AD上时,求![]() 的值.
的值.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)过C点作CF⊥AD,交AD的延长线于F,可证ABCF是正方形,即AB=BC=CF=FA;再由“HL”证得Rt△CBE≌Rt△ CFD,可得BE=FD,最后用线段的和差即可;
(2)分∠EDC=90°和∠DEC=90°两种情况讨论,运用相似三角形的性质和直角三角形的性质即可求解;
(3)连接EM交CD于Q,连接DN交CE于P,连接ED,CM,作CF⊥AD于F,由轴对称的性质可得∠CPD=∠CQE=90°,DC垂直平分EM,可证Rt△CBE≌Rt△CFM,可得BE=FM,由勾股定理可求BE、CE的长,通过证明△CDP∽△CEQ,最后运用相似三角形的性质即可解答.
(1)证明:如图,过C点作CF⊥AD,交AD的延长线于F,
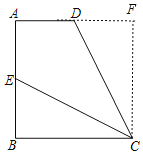
∵AD∥BC,AB⊥BC,AB=BC,
∴四边形ABCF是正方形,
∴AB=BC=CF=FA,
又∵CE=CD,
∴Rt△CBE≌Rt△CFD(HL),
∴BE=FD,
∴AD=AE;
(2)①若∠EDC=90°时,
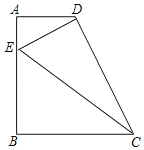
若△ADE、△BCE和△CDE两两相似,
那么∠A=∠B=∠EDC=90°,∠ADE=∠BCE=∠DCE=30°,
在△CBE中,∵BC=1,
∴![]() ,
,![]() ,
,
∵AB=1,
∴![]() ,
,
∴![]() ,
,
此时![]() ≠
≠![]() ,
,
∴△CDE与△ADE、△BCE不相似;
②如图,若∠DEC=90°时,
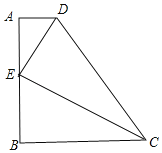
∵∠ADE+∠A=∠BEC+∠DEC,∠DEC=∠A=90°,
∴∠ADE=∠BEC,且∠A=∠B=90°,
∴△ADE∽△BEC,
∴∠AED=∠BCE,
若△CDE与△ADE相似,
∵AB与CD不平行,
∴∠AED与∠EDC不相等,
∴∠AED=∠BCE=∠DCE,
∴若△CDE与△ADE、△BCE相似,
∴![]() ,
,
∴AE=BE,
∵AB=1,
∴AE=BE=![]() ,
,
∴AD=![]() ;
;
(3)连接EM交CD于Q,连接DN交CE于P,连接ED,CM,作CF⊥AD于F,
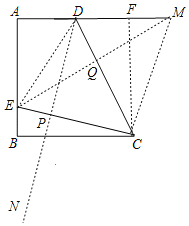
∵E关于直线CD的对称点为M,点D关于直线CE的对称点为N,
∴∠CPD=∠CQE=90°,DC垂直平分EM,
∠PCD=∠QCE,
∴△CDP∽△CEQ,
∴![]() ,
,
∵AD∥BC,AB⊥BC,![]() ,AB=BC=1,
,AB=BC=1,
∴![]() ,
,
∵CD垂直平分EM,
∴DE=DM,CE=CM,
在Rt△CBE和Rt△CFM中,CB=CF,EC=CM,
∴Rt△CBE≌Rt△CFM(HL)
∴BE=FM,
设BE=x,则FM=x,
∵ED=DM,且AE2+AD2=DE2,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵DN=2DP,EM=2EQ,
∴![]() .
.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]()
![]() 的图象交于点
的图象交于点![]() 和
和![]() .
.
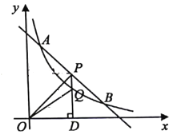
(1)求反比例函数和一次函数的解析式;
(2)点![]() 是线段
是线段![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交反比例函数图象于点
,交反比例函数图象于点![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() 的面积为
的面积为![]() ,求
,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(抗击疫情)为了遏制新型冠状病毒疫情的蔓延势头,各地教育部门在推迟各级学校开学时间的同时提出“听课不停学”的要求,各地学校也都开展了远程网络教学,某校集中为学生提供四类在线学习方式:在线阅读、在线听课、在线答疑、在线讨论,为了了解学生的需求,该校通过网络对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据结果绘制成如下两幅不完整的统计图。

(1)本次调查的人数有多少人?
(2)请补全条形图;
(3)请求出“在线答疑”在扇形图中的圆心角度数;
(4)小宁和小娟都参加了远程网络教学活动,请求出小宁和小娟选择同一种学习方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AC=2,AB=3,BC=4,点G是△ABC的重心.将△ABC平移,使得顶点A与点G重合.那么平移后的三角形与原三角形重叠部分的周长为( )
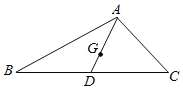
A.2B.3C.4D.4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“长跑”是中考体育考试项目之一.某中学为了解九年级学生“长跑”的情况,随机抽取部分九年级学生,测试其长跑成绩(男子1000米,女子800米),按长跑的时间的长短依次分为A,B,C,D四个等级进行统计,并绘制成如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
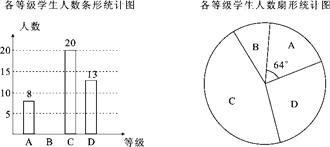
(1)在这次调查中共抽取了 名学生,扇形统计图中,D类所对应的扇形圆心角大小为 ;
(2)所抽取学生“长跑”测试成绩的中位数会落在 等级;
(3)若该校九年级共有900名学生,请你估计该校C等级的学生约在多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
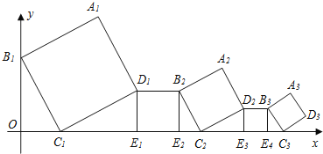
【题目】一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1,E1,E2,C2,E3,E4,C3……在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3……,则正方形A2020B2020C2020D2020的边长是( )
A.(![]() )2017B.(
)2017B.(![]() )2018C.(
)2018C.(![]() )2019D.(
)2019D.(![]() )2020
)2020
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一条直线把一个四边形分成两部分,这两部分图形的周长相等,那么这条直线称为这个四边形的“等分周长线”.在直角梯形ABCD中,AB∥CD,∠A=90°,DC=AD,∠B是锐角,cotB=![]() ,AB=17.如果点E在梯形的边上,CE是梯形ABCD的“等分周长线”,那么△BCE的周长为____.
,AB=17.如果点E在梯形的边上,CE是梯形ABCD的“等分周长线”,那么△BCE的周长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图示,AB是⊙O的直径,点F是半圆上的一动点(F不与A,B重合),弦AD平分∠BAF,过点D作DE⊥AF交射线AF于点AF.
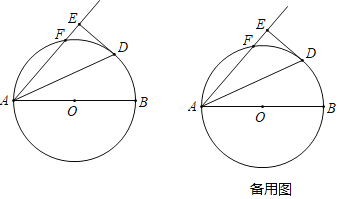
(1)求证:DE与⊙O相切:
(2)若AE=8,AB=10,求DE长;
(3)若AB=10,AF长记为x,EF长记为y,求y与x之间的函数关系式,并求出AFEF的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com