
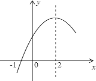
����Ŀ�����κ���y=ax2+bx+c��a��0���IJ���ͼ����ͼ��ʾ��ͼ����㣨-1��0�����Գ���Ϊֱ��x=2�����н��ۣ���1��4a+b=0����2��9a+c��3b����3��8a+7b+2c��0����4������A��-3��y1������B��-![]() ��y2������C��
��y2������C��![]() ��y3���ڸú���ͼ���ϣ���y1��y3��y2����5��������a��x+1����x-5��=-3������Ϊx1��x2����x1��x2����x1��-1��5��x2��������ȷ�Ľ����У�������
��y3���ڸú���ͼ���ϣ���y1��y3��y2����5��������a��x+1����x-5��=-3������Ϊx1��x2����x1��x2����x1��-1��5��x2��������ȷ�Ľ����У�������
A.2��B.3��C.4��D.5��
���𰸡�B
��������
��1����ȷ�����ݶԳ��ṫʽ���㼴�ɣ�
��2����������x����3ʱ��y��0�������жϣ�
��3����ȷ����ͼ���֪�����߾�������1��0���ͣ�5��0�����г����������a��b�����жϣ�
��4���������ú���ͼ���жϣ�
��5����ȷ�����ö��κ�������β���ʽ��ϵ���ɽ�����⣮
�⣺��1����ȷ���ߩ�![]() ��2��
��2��
��4a+b��0������ȷ��
��2������x����3ʱ��y��0��
��9a��3b+c��0��
��9a+c��3b���ʣ�2������
��3����ȷ����ͼ���֪�����߾�������1��0���ͣ�5��0����
��![]() ���
���![]() ��
��
��8a+7b+2c��8a��28a��10a����30a��
��a��0��
��8a+7b+2c��0���ʣ�3����ȷ��
��4�����ߵ�A����3��y1������B����![]() ��y2������C��
��y2������C��![]() ��y3����
��y3����
��![]() ��2��
��2��![]() ��2������
��2������![]() ����
����![]() ��
��
��![]() ��
��![]()
���C��Գ���ľ������
��y3��y2��
��a��0����3����![]() ��2��
��2��
��y1��y2
��y1��y2��y3���ʣ�4������
��5����ȷ����a��0��
�ࣨx+1����x��5����![]() ��0��
��0��
����x+1����x��5����0��
��x����1��x��5���ʣ�5����ȷ��
����ȷ����������
��ѡ��B��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ��ֱ�߰�һ���ı��ηֳ������֣���������ͼ�ε��ܳ���ȣ���ô����ֱ�߳�Ϊ����ı��ε����ȷ��ܳ���������ֱ������ABCD�У�AB��CD����A��90����DC��AD����B����ǣ�cotB��![]() ��AB��17�������E�����εı��ϣ�CE������ABCD�����ȷ��ܳ���������ô��BCE���ܳ�Ϊ____��
��AB��17�������E�����εı��ϣ�CE������ABCD�����ȷ��ܳ���������ô��BCE���ܳ�Ϊ____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼʾ��AB�ǡ�O��ֱ������F�ǰ�Բ�ϵ�һ���㣨F����A��B�غϣ�����ADƽ�֡�BAF������D��DE��AF������AF�ڵ�AF��
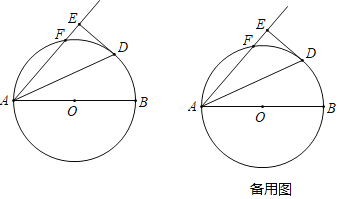
��1����֤��DE���O���У�
��2����AE��8��AB��10����DE����
��3����AB��10��AF����Ϊx��EF����Ϊy����y��x֮��ĺ�����ϵʽ�������AFEF�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
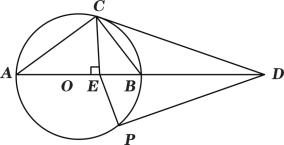
����Ŀ����ͼ��AB�ǡ�O��ֱ����CΪ��O��һ�㣬��CE��AB�ɵ�E��BE=2OE���ӳ�AB����D��ʹ��BD=AB��P�ǻ�AB(����A��B)��һ�����㣬����AC��PE��
��1����AO=3����AC�ij��ȣ�
��2����֤��CD�ǡ�O�����ߣ�
��3����P���˶��Ĺ������Ƿ���ڳ���k��ʹ��PE=k��PD��������ڣ���k��ֵ����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����̵���2Ԫ�������۽���һ������Ʒ.�����鷢�֣�ÿ������3Ԫ��ÿ�����������500�������Ҷ���ÿ����0.1Ԫ����������������10��.���ݹ涨������Ʒ�ۼ۲��ܳ��������۵�2.5��.
��1����ÿ������Ʒ����Ϊ3.5Ԫʱ���̵�ÿ��������________����
��2������̵�Ҫʵ��ÿ��800Ԫ�����������Ǹ���ζ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
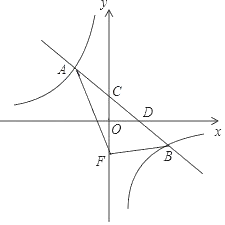
����Ŀ����ƽ��ֱ������ϵ�У�һ�κ���y����![]() x+b��ͼ���뷴��������y��
x+b��ͼ���뷴��������y��![]() ��k��0��ͼ����A��B���㣬��y�ύ�ڵ�C����x�ύ�ڵ�D������A������Ϊ����2��3����
��k��0��ͼ����A��B���㣬��y�ύ�ڵ�C����x�ύ�ڵ�D������A������Ϊ����2��3����
��1����һ�κ����ͷ�������������ʽ��
��2��������C��y������ƽ��4����λ��������F������AF��BF�����ABF�������
��3������ͼ��ֱ��д������ʽ��![]() x+b��
x+b��![]() �Ľ⼯��
�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x�Ķ��κ���y��x2+2kx+k��1������˵����ȷ���ǣ�������
A.������ʵ��k������ͼ����x�ᶼû�н���
B.������ʵ��k������ͼ��û��Ψһ�Ķ���
C.������ʵ��k������ͼ��Ķ�����������y����x2��x��1���˶�
D.������ʵ��k����x�ݩ�k��1ʱ������y��ֵ����x�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪M��N�������y��Գƣ��ҵ�M�ڷ���������![]() ��ͼ���ϣ���N��һ�κ� ��
��ͼ���ϣ���N��һ�κ� ��![]() ��ͼ���ϣ����M������Ϊ��a��b��������κ���
��ͼ���ϣ����M������Ϊ��a��b��������κ���![]() �� ��
�� ��
A.����Сֵ������Сֵ��![]() B.�����ֵ�������ֵ��
B.�����ֵ�������ֵ��![]()
C.�����ֵ�������ֵ��![]() D.����Сֵ������Сֵ��
D.����Сֵ������Сֵ��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���ABCD�������Խ���AC��BD����ƽ�֣���������������һ�����ж��ı���ABCDΪ���ε��ǣ�������
A.��ABD����BDCB.��ABD����BACC.��ABD����CBDD.��ABD����BCA
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com