
【题目】我们知道:有一内角为直角的三角形叫做直角三角形.类似地我们定义:有一内角为45°的三角形叫做半直角三角形.如图,在平面直角坐标系中,O为原点,A(2,0),B(-2,0),D是y轴上的一个动点,∠ADC=90°(A、D、C按顺时针方向排列), BC与经过A、B、D三点的⊙M交于点E,DE平分∠ADC,连结AE,BD.显然ΔDCE、ΔDEF、ΔDAE是半直角三角形.
(1)求证:ΔABC是半直角三角形;
(2)求证:∠DEC=∠DEA;
(3)若点D的坐标为(0,8),求AE的长.

【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】
(1)先求得∠ADE=45°,由同弧所对的圆周角可知:∠ABE=∠ADE=45°,根据定义得:△ABC是半直角三角形;
(2)根据垂直平分线的性质得:AD=BD,由等角对等边得:∠DAB=∠DBA,由D、B、A、E四点共圆,则∠DBA+∠DEA=180°,可得结论;
(3)设⊙M的半径为r,根据勾股定理列方程为:(8﹣r)2+22=r2,可得⊙M 的半径为![]() ,由同弧所对的圆心角和圆周角的关系可得∠EMA=2∠ABE=90°,根据勾股定理可得结论.
,由同弧所对的圆心角和圆周角的关系可得∠EMA=2∠ABE=90°,根据勾股定理可得结论.
解:(1)∵∠ADC=90°,DE平分∠ADC,
∴∠ADE=45°,
∵∠ABE=∠ADE=45°,
∴△ABC是半直角三角形;
(2)∵OM⊥AB,OA=OB,
∴AD=BD,
∴∠DAB=∠DBA,
∵∠DEB=∠DAB,
∴∠DBA=∠DEB,
∵D、B、A、E四点共圆,
∴∠DBA+∠DEA=180°,
∵∠DEB+∠DEC=180°,
∴∠DEA=∠DEC;
(3)①如图1,连接AM,ME,
设⊙M的半径为r,
∵点D的坐标为(0,8),
∴OM=8﹣r,
由OM2+OA2=MA2得:(8﹣r)2+22=r2,
解得r=![]() ,
,
∴⊙M 的半径为![]() ,
,
∵∠ABE=45°
∴∠EMA=2∠ABE=90°,
∴EA2=MA2+ME2=(![]() )2+(
)2+(![]() )2,
)2,
∴![]()



 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣
x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过点A,B.
x2+bx+c经过点A,B.
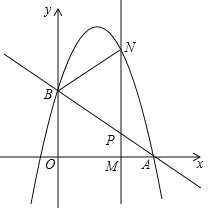
(1)求点B的坐标和抛物线的解析式;
(2)M(m,0)为线段OA上一个动点,过点M垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
①试用含m的代数式表示线段PN的长;
②求线段PN的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区商店以2元的批发价进了一批纪念品.经调查发现,每个定价3元,每天可以能卖出500件,而且定价每上涨0.1元,其销售量将减少10件.根据规定:纪念品售价不能超过批发价的2.5倍.
(1)当每个纪念品定价为3.5元时,商店每天能卖出________件;
(2)如果商店要实现每天800元的销售利润,那该如何定价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一方有难,八方支援”.四川汶川大地震牵动着全国人民的心,我市某医院准备从甲、乙、丙三位医生和A、B两名护士中选取一位医生和一名护士支援汶川.
(1)若随机选一位医生和一名护士,用树状图(或列表法)表示所有可能出现的结果;
(2)求恰好选中医生甲和护士A的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的二次函数y=x2+2kx+k﹣1,下列说法正确的是( )
A.对任意实数k,函数图象与x轴都没有交点
B.对任意实数k,函数图象没有唯一的定点
C.对任意实数k,函数图象的顶点在抛物线y=﹣x2﹣x﹣1上运动
D.对任意实数k,当x≥﹣k﹣1时,函数y的值都随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级数学兴趣小组在研究等腰直角三角形与图形变换时,作了如下研究:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为腰作等腰直角三角形DAF,使∠DAF=90°,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①CF与BC的位置关系为 ;
②CF,DC,BC之间的数量关系为 (直接写出结论);
(2)数学思考
如图2,当点D在线段CB的延长线上时,(1)中的①、②结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,将△DAF沿线段DF翻折,使点A与点E重合,连接CE,若已知4CD=BC,AC=2![]() ,请求出线段CE的长.
,请求出线段CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a<0,a、b、c为常数)与x轴交于A、C两点,与y轴交于B点,A(﹣6,0),C(1,0),B(0,![]() ).
).
(1)求该抛物线的函数关系式与直线AB的函数关系式;
(2)已知点M(m,0)是线段OA上的一个动点,过点M作x轴的垂线l,分别与直线AB和抛物线交于D、E两点,当m为何值时,△BDE恰好是以DE为底边的等腰三角形?
(3)在(2)问条件下,当△BDE恰妤是以DE为底边的等腰三角形时,动点M相应位置记为点M',将OM'绕原点O顺时针旋转得到ON(旋转角在0°到90°之间);
①探究:线段OB上是否存在定点P(P不与O、B重合),无论ON如何旋转,![]() 始终保持不变,若存在,试求出P点坐标:若不存在,请说明理由;
始终保持不变,若存在,试求出P点坐标:若不存在,请说明理由;
②试求出此旋转过程中,(NA![]() NB)的最小值.
NB)的最小值.
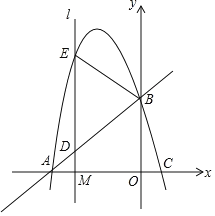
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知半圆⊙O的直径AB=10,弦CD∥AB,且CD=8,E为弧CD的中点,点P在弦CD上,联结PE,过点E作PE的垂线交弦CD于点G,交射线OB于点F.
(1)当点F与点B重合时,求CP的长;
(2)设CP=x,OF=y,求y与x的函数关系式及定义域;
(3)如果GP=GF,求△EPF的面积.
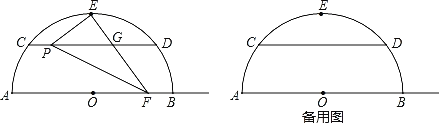
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com