
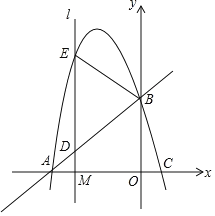
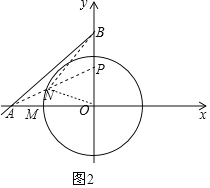
【题目】如图,抛物线y=ax2+bx+c(a<0,a、b、c为常数)与x轴交于A、C两点,与y轴交于B点,A(﹣6,0),C(1,0),B(0,![]() ).
).
(1)求该抛物线的函数关系式与直线AB的函数关系式;
(2)已知点M(m,0)是线段OA上的一个动点,过点M作x轴的垂线l,分别与直线AB和抛物线交于D、E两点,当m为何值时,△BDE恰好是以DE为底边的等腰三角形?
(3)在(2)问条件下,当△BDE恰妤是以DE为底边的等腰三角形时,动点M相应位置记为点M',将OM'绕原点O顺时针旋转得到ON(旋转角在0°到90°之间);
①探究:线段OB上是否存在定点P(P不与O、B重合),无论ON如何旋转,![]() 始终保持不变,若存在,试求出P点坐标:若不存在,请说明理由;
始终保持不变,若存在,试求出P点坐标:若不存在,请说明理由;
②试求出此旋转过程中,(NA![]() NB)的最小值.
NB)的最小值.
【答案】y![]() x2
x2![]() x
x![]() ,直线AB的解析式为:y
,直线AB的解析式为:y![]() x
x![]() ;(2)当m=﹣4时,△BDE恰好是以DE为底边的等腰三角形;(3)①存在,P(0,3);②
;(2)当m=﹣4时,△BDE恰好是以DE为底边的等腰三角形;(3)①存在,P(0,3);②![]() .
.
【解析】
(1)根据A和C的坐标设出两点式,再代入点B的坐标,即可求出抛物线的解析式;设直线AB的解析式为y=kx+n,将A和B的坐标代入求解,即可得出直线AB的解析式;
(2)根据点M的坐标写出点D的坐标,作BG⊥DE于点D得出GM=OB![]() ,代入求解即可得出答案;
,代入求解即可得出答案;
(3)①假设存在,证出△NOP∽△BON得出![]() 即可得出答案;②结合①得出(NA
即可得出答案;②结合①得出(NA![]() NB)的最小值=NA+NP,此时N,A,P三点共线,计算即可得出答案.
NB)的最小值=NA+NP,此时N,A,P三点共线,计算即可得出答案.
解:(1)设抛物线解析式为y= a(x+6)(x﹣1),(a≠0).
将B(0,![]() )代入,得
)代入,得![]() a(x+6)(x﹣1),
a(x+6)(x﹣1),
解得:a![]() ,
,
∴该抛物线解析式为y![]() (x+6)(x﹣1)或y
(x+6)(x﹣1)或y![]() x2
x2![]() x
x![]() .
.
设直线AB的解析式为y=kx+n(k≠0).
将点A(﹣6,0),B(0,![]() )代入,得
)代入,得
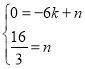 ,
,
解得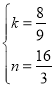 ,
,
则直线AB的解析式为:y![]() x
x![]() ;
;
(2)∵点M(m,0),过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点,∴D(m,![]() m
m![]() ),
),
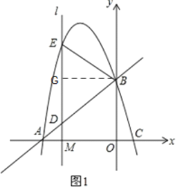
当DE为底时,如图1,作BG⊥DE于G,则EG=GD![]() ED,GM=OB
ED,GM=OB![]() ,
,
∵DM+DG=GM=OB,
∴![]() m
m![]() (
(![]() m2
m2![]() m
m![]() m
m![]() )
)![]() ,
,
解得:m1=﹣4,m2=0(不合题意,舍去),
∴当m=﹣4时,△BDE恰好是以DE为底边的等腰三角形;
(3)①存在,如图2.
∵ON=OM'=4,OB![]() ,
,
∵∠NOP=∠BON,
∴当△NOP∽△BON时,![]() ,
,
∴![]() 不变,
不变,
即OP![]() ON
ON![]() 4=3,
4=3,
∴P(0,3);
②∵N在以O为圆心,4为半径的半圆上,由①知,![]() ,
,
∴NP![]() NB,
NB,
∴(NA![]() NB)的最小值=NA+NP,
NB)的最小值=NA+NP,
∴此时N,A,P三点共线,
∴(NA![]() NB)的最小值
NB)的最小值![]() 3
3![]() .
.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】我们知道:有一内角为直角的三角形叫做直角三角形.类似地我们定义:有一内角为45°的三角形叫做半直角三角形.如图,在平面直角坐标系中,O为原点,A(2,0),B(-2,0),D是y轴上的一个动点,∠ADC=90°(A、D、C按顺时针方向排列), BC与经过A、B、D三点的⊙M交于点E,DE平分∠ADC,连结AE,BD.显然ΔDCE、ΔDEF、ΔDAE是半直角三角形.
(1)求证:ΔABC是半直角三角形;
(2)求证:∠DEC=∠DEA;
(3)若点D的坐标为(0,8),求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
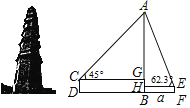
【题目】慈氏塔位于岳阳市城西洞庭湖边,是湖南省保存最好的古塔建筑之一.如图,小亮的目高CD为1.7米,他站在D处测得塔顶的仰角∠ACG为45°,小琴的目高EF为1.5米,她站在距离塔底中心B点a米远的F处,测得塔顶的仰角∠AEH为62.3°.(点D、B、F在同一水平线上,参考数据:sin62.3°≈0.89,cos62.3°≈0.46,tan62.3°≈1.9)
(1)求小亮与塔底中心的距离BD;(用含a的式子表示)
(2)若小亮与小琴相距52米,求慈氏塔的高度AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“书香学校,书香班级”的建设号召,平顶山市某中学积极行动,学校图书角的新书、好书不断增加.下面是随机抽查该校若干名同学捐书情况统计图:
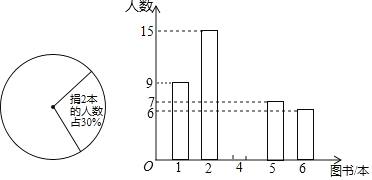
请根据下列统计图中的信息,解答下列问题:
(1)此次随机调查同学所捐图书数的中位数是 ,众数是 ;
(2)在扇形统计图中,捐2本书的人数所占的扇形圆心角是多少度?
(3)若该校有在校生1600名学生,估计该校捐4本书的学生约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() (k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.
(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.
(1)求这个反比函数的表达式;
(2)求△ACD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 抛物线![]() 与
与![]() 轴交于点A(-1,0),顶点坐标(1,n)与
轴交于点A(-1,0),顶点坐标(1,n)与![]() 轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①
轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①![]() ;②
;②![]() ;③对于任意实数m,
;③对于任意实数m,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 有两个不相等的实数根.其中结论正确的个数为
有两个不相等的实数根.其中结论正确的个数为![]()
![]()

A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
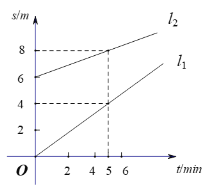
【题目】探测气球甲从海拔![]() 处出发,与此同时,探测气球乙从海拔
处出发,与此同时,探测气球乙从海拔![]() 处出发.图中的
处出发.图中的![]() 分别表示甲、乙两个气球所在位置的海拔
分别表示甲、乙两个气球所在位置的海拔![]() (单位:
(单位:![]() )与上升时间
)与上升时间![]() (单位:
(单位:![]() )之间的关系.
)之间的关系.
(1)求![]() 的函数解析式;
的函数解析式;
(2)探测气球甲从出发点上升到海拔![]() 处的过程中,是否存在某一时刻使得探测气球甲、乙位于同一高度?请说明理由.
处的过程中,是否存在某一时刻使得探测气球甲、乙位于同一高度?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
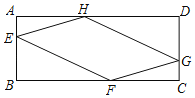
【题目】如图,点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA(不包括端点)上运动,且满足![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)试判断四边形EFGH的形状,并说明理由.
(3)请探究四边形EFGH的周长一半与矩形ABCD一条对角线长的大小关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com