
【题目】探测气球甲从海拔![]() 处出发,与此同时,探测气球乙从海拔
处出发,与此同时,探测气球乙从海拔![]() 处出发.图中的
处出发.图中的![]() 分别表示甲、乙两个气球所在位置的海拔
分别表示甲、乙两个气球所在位置的海拔![]() (单位:
(单位:![]() )与上升时间
)与上升时间![]() (单位:
(单位:![]() )之间的关系.
)之间的关系.
(1)求![]() 的函数解析式;
的函数解析式;
(2)探测气球甲从出发点上升到海拔![]() 处的过程中,是否存在某一时刻使得探测气球甲、乙位于同一高度?请说明理由.
处的过程中,是否存在某一时刻使得探测气球甲、乙位于同一高度?请说明理由.
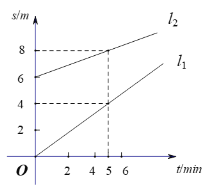
【答案】(1)s=![]() t+6(t≥0);(2)探测气球甲从出发点上升到海拔16m处的过程中,当上升15min时探测气球甲、乙位于同一高度,见解析
t+6(t≥0);(2)探测气球甲从出发点上升到海拔16m处的过程中,当上升15min时探测气球甲、乙位于同一高度,见解析
【解析】
(1)设l2的解析式为s=k2t+b(k2≠0),根据t=0时,s=6、当t=5时,s=8直接列方程组,求解即可;
(2)先根据题意求出![]() 的解析式,联立l1和l2,求出此时的t值,经验证满足题意,即可求解本题.
的解析式,联立l1和l2,求出此时的t值,经验证满足题意,即可求解本题.
(1)解:由题可设l2的解析式为s=k2t+b(k2≠0)
因为当t=0时,s=6、当t=5时,s=8,
代入得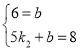 ,
,
解得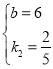 ,
,
所以l2:s=![]() t+6(t≥0);
t+6(t≥0);
(2)解:由题可设l1:s=k1t(k1≠0),
因为当t=5时,s=4,
代入可得l1:s=![]() t(t≥0)
t(t≥0)
当二者处于同一高度时,
![]() t+6=
t+6=![]() t,
t,
解得t=15,
此时s=12,
即在15min时,二者处于同一高度12m;
因为12m<16m,
所以探测气球甲从出发点上升到海拔16m处的过程中,当上升15min时,探测气球甲、乙位于同一高度;
答:探测气球甲从出发点上升到海拔16m处的过程中,当上升15min时探测气球甲甲、乙位于同一高度.


科目:初中数学 来源: 题型:
【题目】某景区商店以2元的批发价进了一批纪念品.经调查发现,每个定价3元,每天可以能卖出500件,而且定价每上涨0.1元,其销售量将减少10件.根据规定:纪念品售价不能超过批发价的2.5倍.
(1)当每个纪念品定价为3.5元时,商店每天能卖出________件;
(2)如果商店要实现每天800元的销售利润,那该如何定价?
查看答案和解析>>
科目:初中数学 来源: 题型:
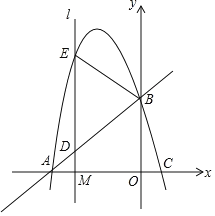
【题目】如图,抛物线y=ax2+bx+c(a<0,a、b、c为常数)与x轴交于A、C两点,与y轴交于B点,A(﹣6,0),C(1,0),B(0,![]() ).
).
(1)求该抛物线的函数关系式与直线AB的函数关系式;
(2)已知点M(m,0)是线段OA上的一个动点,过点M作x轴的垂线l,分别与直线AB和抛物线交于D、E两点,当m为何值时,△BDE恰好是以DE为底边的等腰三角形?
(3)在(2)问条件下,当△BDE恰妤是以DE为底边的等腰三角形时,动点M相应位置记为点M',将OM'绕原点O顺时针旋转得到ON(旋转角在0°到90°之间);
①探究:线段OB上是否存在定点P(P不与O、B重合),无论ON如何旋转,![]() 始终保持不变,若存在,试求出P点坐标:若不存在,请说明理由;
始终保持不变,若存在,试求出P点坐标:若不存在,请说明理由;
②试求出此旋转过程中,(NA![]() NB)的最小值.
NB)的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】投资1万元围一个矩形菜园(如图),其中一边靠墙,另外三边选用不同材料建造.墙长24 m,平行于墙的边的费用为200元/m,垂直于墙的边的费用为150元/m,设平行于墙的边长为x m.
(1)设垂直于墙的一边长为y m,直接写出y与x之间的函数关系式;
(2)若菜园面积为384 m2,求x的值;
(3)求菜园的最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
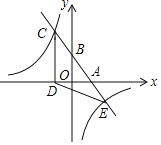
【题目】如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD的两条对角线AC、BD互相平分.添加下列条件,一定能判定四边形ABCD为菱形的是( )
A.∠ABD=∠BDCB.∠ABD=∠BACC.∠ABD=∠CBDD.∠ABD=∠BCA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知半圆⊙O的直径AB=10,弦CD∥AB,且CD=8,E为弧CD的中点,点P在弦CD上,联结PE,过点E作PE的垂线交弦CD于点G,交射线OB于点F.
(1)当点F与点B重合时,求CP的长;
(2)设CP=x,OF=y,求y与x的函数关系式及定义域;
(3)如果GP=GF,求△EPF的面积.
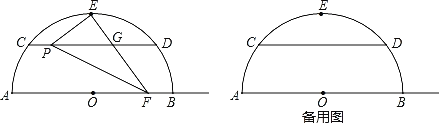
查看答案和解析>>
科目:初中数学 来源: 题型:
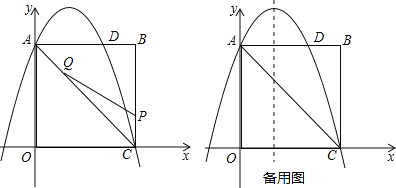
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 2
D. 2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com