
【题目】已知抛物线y=x2+bx﹣3经过点A(1,0),顶点为点M.
(1)求抛物线的表达式及顶点M的坐标;
(2)求∠OAM的正弦值.
【答案】(1)M的坐标为(﹣1,﹣4);(2)![]() .
.
【解析】
(1)把A坐标代入抛物线解析式求出b的值,确定出抛物线表达式,并求出顶点坐标即可;
(2)根据(1)确定出抛物线对称轴,求出抛物线与x轴的交点B坐标,根据题意得到三角形AMB为直角三角形,由MB与AB的长,利用勾股定理求出AM的长,再利用锐角三角函数定义求出所求即可.
解:(1)由题意,得1+b﹣3=0,
解这个方程,得,b=2,
所以,这个抛物线的表达式是y=x2+2x﹣3,
所以y=(x+1)2﹣4,
则顶点M的坐标为(﹣1,﹣4);
(2)由(1)得:这个抛物线的对称轴是直线x=﹣1,
设直线x=-1与x轴的交点为点B,
则点B的坐标为(﹣1,0),且∠MBA=90°,
在Rt△ABM中,MB=4,AB=2,
由勾股定理得:AM2=MB2+AB2=16+4=20,即AM=2![]() ,
,
所以sin∠OAM=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】某条道路上通行车辆限速为60千米/时,在离道路50米的点P处建一个监测点,道路AB段为检测区(如图).在△ABP中,已知∠PAB=30°,∠PBA=45°,一辆轿车通过AB段的时间8.1秒,请判断该车是否超速?(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,60千米/时=
≈1.73,60千米/时=![]() 米/秒)
米/秒)
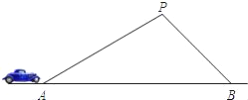
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣2x﹣8.
(1)用配方法把y=x2﹣2x﹣8化为y=(x﹣h)2+k形式;
(2)并指出:抛物线的顶点坐标是 ,抛物线的对称轴方程是 ,抛物线与x轴交点坐标是 ,当x 时,y随x的增大而增大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件
B.甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是![]() ,
,![]() ,则甲的射击成绩较稳定
,则甲的射击成绩较稳定
C.“明天降雨的概率为![]() ”,表示明天有半天都在降雨
”,表示明天有半天都在降雨
D.了解一批电视机的使用寿命,适合用普查的方式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).
(1)求该抛物线所对应的函数关系式;
(2)设抛物线上的一个动点P的横坐标为t(0<t<3),过点P作PD⊥BC于点D. ① 求线段PD的长的最大值;② 当BD=2CD时,求t的值;
(3)若点Q是抛物线的对称轴上的动点,抛物线上存在点M,使得以B、C、Q、M为顶点的四边形为平行四边形,请求出所有满足条件的点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图2,![]() 与
与![]() 是两个全等的等腰三角形,
是两个全等的等腰三角形,![]() ,
,![]() 分别与
分别与![]() 相交于点
相交于点![]() ,
,![]() .
.

(1)图中有哪几对不全等的相似三角形,请把他们表示出来;
(2)根据图1两位同学对图形的探索,试探索![]() 之间的关系,并证明.
之间的关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线y=ax2(a≠0)与一次函数y=kx+b的图象相交于A(﹣1,﹣1),B(2,﹣4)两点,点P是抛物线上不与A,B重合的一个动点,点Q是y轴上的一个动点.
(1)请直接写出a,k,b的值及关于x的不等式ax2<kx﹣2的解集;
(2)当点P在直线AB上方时,请求出△PAB面积的最大值并求出此时点P的坐标;
(3)是否存在以P,Q,A,B为顶点的四边形是平行四边形?若存在,请直接写出P,Q的坐标;若不存在,请说明理由.
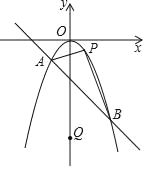
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O′在第一象限,⊙O′与x轴相切于H点,与y轴相交于A(0,2),B(0,8),则点O′的坐标是( )

A. (6,4) B. (4,6) C. (5,4) D. (4,5)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com