
����Ŀ��ijУ���꼶��ѧ��ȤС�����о�����ֱ����������ͼ�α任ʱ�����������о����ڡ�ABC�У���BAC��90�㣬AB��AC����DΪֱ��BC��һ���㣨��D����B��C�غϣ�����ADΪ��������ֱ��������DAF��ʹ��DAF��90�㣬����CF��
��1���۲����
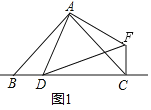
��ͼ1������D���߶�BC��ʱ��
��CF��BC��λ�ù�ϵΪ�� ����
��CF��DC��BC֮���������ϵΪ�� ����ֱ��д�����ۣ���
��2����ѧ˼��
��ͼ2������D���߶�CB���ӳ�����ʱ����1���е������������Ƿ���Ȼ�������������������֤������������������д����ȷ�����ٸ���֤����
��3����չ����
��ͼ3������D���߶�BC���ӳ�����ʱ������DAF���߶�DF���ۣ�ʹ��A���E�غϣ�����CE������֪4CD��BC��AC��2![]() ��������߶�CE�ij���
��������߶�CE�ij���

���𰸡���1���ٴ�ֱ����BC��CF+CD����2��CF��BC������BC��CD+CF�����������ۣ�CD��CF+BC�����ɼ���������3��CE��3![]() ��
��
��������
��1�����ɡ�BAC����DAF��90�㣬�Ƴ���DAB�ա�FAC������ȫ�������ε����ʼ��ɵõ����ۣ�����������ADEF�����ʿ��Ƴ���DAB�ա�FAC������ȫ�������ε����ʵõ�CF��BD����ACF����ABD��������ǵ����ʼ��ɵõ����ۣ�
��2���ɡ�BAC����DAF��90�㣬�Ƴ���DAB�ա�FAC������ȫ�������ε������Լ�����ֱ�������εĽǵ����ʿɵõ����ۣ�
��3����A��AH��BC��H����E��EM��BD��M��ͼ3��ʾ����취֤����ADH�ա�DEM��AAS�����Ƴ�EM��DH��3��DM��AH��2���Ƴ�CM��EM��3�����ɽ�����⣮
�⣺��1����
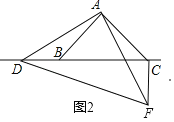
����ֱ����ADF�У�AD��AF��
�ߡ�BAC����DAF��90����
���BAD����CAF��
����DAB����FAC��
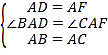 ��
��
���DAB�ա�FAC��SAS����
���B����ACF��
���ACB+��ACF��90������BC��CF��
�ڡ�DAB�ա�FAC��
��CF��BD��
��BC��BD+CD��
��BC��CF+CD��
�ʴ�Ϊ����ֱ��BC��CF+CD��
��2��CF��BC������BC��CD+CF�����������ۣ�CD��CF+BC���������£�
������ֱ����ADF�У�AD��AF��
�ߡ�BAC����DAF��90����
���BAD����CAF��
����DAB����FAC��
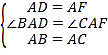 ��
��
���DAB�ա�FAC��SAS����
���ABD����ACF��
�ߡ�BAC��90����AB��AC��
���ACB����ABC��45����
���ABD��180����45����135����
���BCF����ACF����ACB��135����45����90����
��CF��BC��
��CD��DB+BC��DB��CF��
��CD��CF+BC��
��3����A��AH��BC��H����E��EM��BD��M��ͼ3��ʾ��
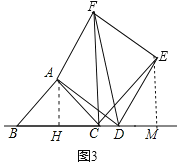
�ߡ�BAC��90����AB��AC��2![]() ��
��
��BC��![]() AB��4��AH��BH��CH��
AB��4��AH��BH��CH��![]() BC��2��
BC��2��
��CD��![]() BC��1��
BC��1��
��DH��CH+CD��3��
���ı���ADEF�������Σ�
��AD��DE����ADE��90����
��BC��CF��EM��BD��EN��CF��
���ı���CMEN�Ǿ��Σ�
��NE��CM��EM��CN��
�ߡ�AHD����ADC����EMD��90����
���ADH+��EDM����EDM+��DEM��90����
���ADH����DEM��
����ADH����DEM��
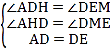 ��
��
���ADH�ա�DEM��AAS����
��EM��DH��3��DM��AH��2��
��CM��EM��3��
��CE��![]() ��3
��3![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ҵ���ָ���Ƿ�ӳһ�����ҿ�ѧ�����ʹ��¾��������ۺ�ָ�����Թ��Ҵ���ָ���÷�����ǰ40�Ĺ��ҵ��й����ݽ����ռ��������������ͷ�������������˲�����Ϣ��
a�����Ҵ���ָ���÷ֵ�Ƶ���ֲ�ֱ��ͼ�����ݷֳ�7�飺
30��x��40��40��x��50��50��x��60��60��x��70��70��x��80��80��x��90��90��x��100����
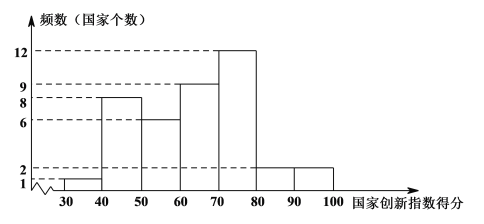
b�����Ҵ���ָ���÷���60��x��70��һ����ǣ�61.7 62.4 63.6 65.9 66.4 68.5 69.1 69.3 69.5
c��40�����ҵ��˾�����������ֵ���Ҵ���ָ���÷����ͳ��ͼ��
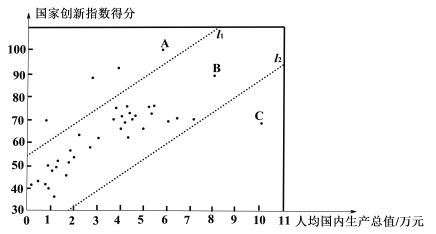
d���й��Ĺ��Ҵ���ָ���÷�Ϊ69.5.
������������Դ�ڡ����Ҵ���ָ�����棨2018������
����������Ϣ���ش��������⣺
��1���й��Ĺ��Ҵ���ָ���÷����������______��
��2����40�����ҵ��˾�����������ֵ���Ҵ���ָ���÷����ͳ��ͼ�У������й����ڵ�����������������Ӧ�ĵ�λ������![]() ���Ϸ�������ͼ������
���Ϸ�������ͼ������![]() ��Ȧ�������й��ĵ㣻
��Ȧ�������й��ĵ㣻
��3���ڹ��Ҵ���ָ���÷ֱ��й��ߵĹ����У��˾�����������ֵ����СֵԼΪ______����Ԫ�����������һλС����
��4�������ƶϺ�������______��
������ڵ�A��B�������Ĺ��ң��й��Ĺ��Ҵ���ָ���÷ֻ���һ����࣬�й�������ӿ콨�贴����������ս������һ����߹����ۺϴ���������
������ڵ�B��C�������Ĺ��ң��й����˾�����������ֵ����һ����࣬�й��������ʤȫ�潨��С��������ķܶ�Ŀ�꣬��һ������˾�����������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���D��E��F�ֱ��DZ�AB��AC��BC���е㣬Ҫ�ж��ı���DBFE�����Σ�������������������ȷ���ǣ�������

A. AB=AC B. AB=BC C. BEƽ�֡�ABC D. EF=CF
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪������һ�ڽ�Ϊֱ�ǵ������ν���ֱ�������Σ����Ƶ����Ƕ��壺��һ�ڽ�Ϊ45���������ν�����ֱ�������Σ���ͼ����ƽ��ֱ������ϵ�У�OΪԭ�㣬A��2��0����B����2��0����D��y���ϵ�һ�����㣬��ADC=90��(A��D��C��˳ʱ�뷽������)�� BC�뾭��A��B��D�������M���ڵ�E��DEƽ����ADC������AE��BD����Ȼ��DCE����DEF����DAE�ǰ�ֱ�������Σ�
��1����֤����ABC�ǰ�ֱ�������Σ�
��2����֤����DEC=��DEA��
��3������D��������0��8������AE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
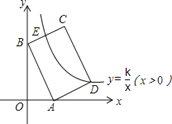
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABCD�ı�AB��BC=3��2����A��3��0����B��0��6���ֱ���x�ᣬy���ϣ�����������y=![]() ��x��0����ͼ����D�������BC���ڵ�E�����E������Ϊ__��
��x��0����ͼ����D�������BC���ڵ�E�����E������Ϊ__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
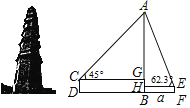
����Ŀ��������λ�������г�����ͥ���ߣ��Ǻ���ʡ������õĹ�������֮һ.��ͼ��С����Ŀ��CDΪ1.7�ף���վ��D��������������ǡ�ACGΪ45�㣬С�ٵ�Ŀ��EFΪ1.5�ף���վ�ھ�����������B��a��Զ��F����������������ǡ�AEHΪ62.3��.(��D��B��F��ͬһˮƽ���ϣ��ο����ݣ�sin62.3���0.89��cos62.3���0.46��tan62.3���1.9)
(1)��С�����������ĵľ���BD��(�ú�a��ʽ�ӱ�ʾ)
(2)��С����С�����52�ף���������ĸ߶�AB.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��Ӧ������ѧУ������༶���Ľ�����٣�ƽ��ɽ��ij��ѧ�����ж���ѧУͼ��ǵ����顢���鲻�����ӣ��������������У������ͬѧ�������ͳ��ͼ��
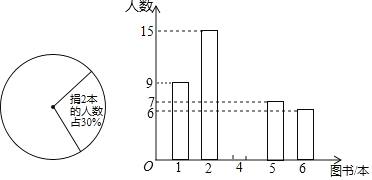
���������ͳ��ͼ�е���Ϣ������������⣺
��1���˴��������ͬѧ����ͼ��������λ������ ������������ ����
��2��������ͳ��ͼ�У���2�����������ռ������Բ�Ľ��Ƕ��ٶȣ�
��3������У����У��1600��ѧ�������Ƹ�У��4�����ѧ��Լ�ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�� ������![]() ��
��![]() �ύ�ڵ�A��-1,0�����������꣨1��n����
�ύ�ڵ�A��-1,0�����������꣨1��n����![]() ��Ľ����ڣ�0,2������0,3��֮�䣨�� ���˵㣩�������н��ۣ���
��Ľ����ڣ�0,2������0,3��֮�䣨�� ���˵㣩�������н��ۣ���![]() ����
����![]() ���۶�������ʵ��m��
���۶�������ʵ��m��![]() �ܳ������ܹ���
�ܳ������ܹ���![]() �ķ���
�ķ���![]() ����������ȵ�ʵ���������н�����ȷ�ĸ���Ϊ
����������ȵ�ʵ���������н�����ȷ�ĸ���Ϊ![]() ����
����![]()

A. 1 �� B. 2 �� C. 3 �� D. 4 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ٵ�һ�����ӣ�����һ���ֻ�!������2017����Ȧһƪ�ȴ������£������ϣ����������������� 2018 ��9����ѧ����Сѧ�ͳ��н�ֹѧ��ʹ���ֻ���Ϊ�˽�ѧ���ֻ�ʹ�������ijѧУ��չ�����ֻ����ҽ����������������������ȡ����ѧ��������ʹ���ֻ�Ŀ��������ÿ��ʹ���ֻ���ʱ�������ʾ����飬�����Ƴ���ͼ�٣��ڵ� ͳ��ͼ����֪������������������ 40�ˣ��������������Ϣ����������⣺
(1)������ͳ��ͼ�У�������Ϸ����Ӧ�İٷֱ�Ϊ______��Բ�ĽǶ�����______�ȣ�
(2)��ȫ����ͳ��ͼ��
(3)��У����ѧ��2100�ˣ�����ÿ��ʹ���ֻ�ʱ����2 Сʱ����(����2Сʱ)��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com