
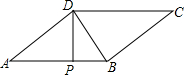
 如图,?ABCD中,DP⊥AB于P,且PD2=AP•PB,△BCD的面积和周长分别为24和24,求PD的长.
如图,?ABCD中,DP⊥AB于P,且PD2=AP•PB,△BCD的面积和周长分别为24和24,求PD的长. 分析 将等积式PD2=AP•PB化为等比式$\frac{PD}{AP}$=$\frac{PB}{PD}$,得到△DAP∽△BDP,设AD=a,BD=b,AB=c,列出方程组$\left\{\begin{array}{l}ab=48\\ a+b+c=24\\{a}^{2}+{b}^{2}{=c}^{2}\end{array}\right.$即可解答.
解答 解:∵PD2=AP•PB,
∴$\frac{PD}{AP}$=$\frac{PB}{PD}$,
又∵DP⊥AB于P,
∴∠DPA=∠DPB,
∴△DAP∽△BDP,
∴∠ADB=90°,
设AD=a,BD=b,AB=c,
由题意得,$\left\{\begin{array}{l}ab=48\\ a+b+c=24\\{a}^{2}+{b}^{2}{=c}^{2}\end{array}\right.$,
解得,AB=c=10,
∵$\frac{1}{2}$DP•AB=$\frac{1}{2}$AD•DB=$\frac{1}{2}$×48=24,
∴PD=4.8.
点评 本题考查了相似三角形的判定与性质、平行四边形的性质,找到△DAP∽△BDP并利用相似三角形的性质找到相等的直角是解题的关键.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
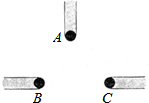 (1)如图是小刚(A)、小明(B)、小勇(C)和他们各自影子的俯视图,他们所构成三角形地形的内部有一盏路灯,你认为如图是在白天阳光下的俯视图还是在晚上这盏路灯下的俯视图?
(1)如图是小刚(A)、小明(B)、小勇(C)和他们各自影子的俯视图,他们所构成三角形地形的内部有一盏路灯,你认为如图是在白天阳光下的俯视图还是在晚上这盏路灯下的俯视图?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
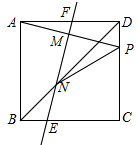 如图,正方形ABCD中,点P为CD上一点,线段AP的垂直平分线MN交BD于点N,点M为垂足,交两边于点E、F,连接PN,则下列结论,其中正确的有( )
如图,正方形ABCD中,点P为CD上一点,线段AP的垂直平分线MN交BD于点N,点M为垂足,交两边于点E、F,连接PN,则下列结论,其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
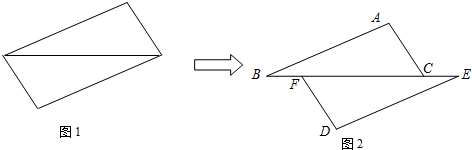
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
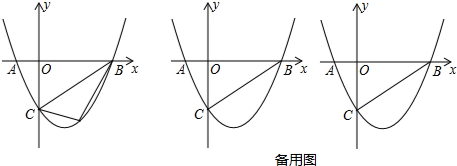
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com