
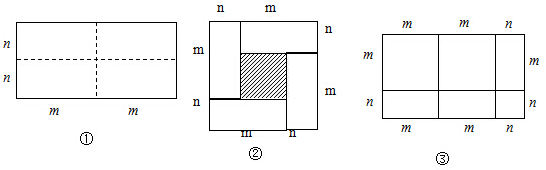
分析 (1)阴影部分的边长为小长方形的长减去宽,即m-n,各角均为直角,可得;
(2)根据大正方形面积等于边长的平方或小正方形面积加4个小长方形面积的两种不同算法,可得等式;
(3)根据大长方形面积等于长乘以宽或6个矩形面积和的两种不同算法可列出等式.
解答 解:(1)图②中阴影部分的边长都等于小长方形的长减去小长方形的宽,即m-n,
由图可知,阴影部分的四个角都是直角,故阴影部分是正方形,其边长为m-n;
(2)大正方形的面积边长的平方,即(m+n)2,或小正方形面积加4个小长方形的面积,即4mn+(m-n)2,
故可得:(m+n)2=(m-n)2+4mn;
(3)大长方形的面积为长×宽,即(2m+n)(m+n),
或者分割成6个矩形的面积和,即m2+3mn+n2,
故(2m+n)(m+n)=2m2+3mn+n2;
故答案为:(1)正方,m-n,(2)(m+n)2=(m-n)2+4mn,(3)(2m+n)(m+n)=2m2+3mn+n2.
点评 本题考查了完全平方公式的几何背景,属于基础题,注意仔细观察图形,表示出各图形的面积是关键.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在△ABC中,∠ABC的平分线BP与AC边的垂直平分线PQ交于点P,过点P分别作PD⊥AB于点D,PE⊥BC于点E,若BE=10cm,AB=6cm,求CE的长.
已知:如图,在△ABC中,∠ABC的平分线BP与AC边的垂直平分线PQ交于点P,过点P分别作PD⊥AB于点D,PE⊥BC于点E,若BE=10cm,AB=6cm,求CE的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{36}$=±6 | B. | $\sqrt{(-3{)^2}}$=-3 | C. | -$\root{3}{-\frac{8}{125}}$=$\frac{2}{5}$ | D. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}x=-1\\ y=2\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=1\\ y=2\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=1\\ y=-2\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=-1\\ y=-2\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com