
 如图,抛物线与x轴交于B、C两点(点B在点C的右侧),其顶点为点A(1,4),且抛物线经过点B(4,0).
如图,抛物线与x轴交于B、C两点(点B在点C的右侧),其顶点为点A(1,4),且抛物线经过点B(4,0).| 4 |
| 9 |
| 4 |
| 9 |

| AE2+BE2 |
| 42+(4-1)2 |
| PB |
| AB |
| BQ |
| BE |
| 6-t |
| 5 |
| t |
| 3 |
| 9 |
| 4 |

| AE2+BE2 |
| 42+(4-1)2 |
| PB |
| EB |
| BQ |
| BA |
| 6-t |
| 3 |
| t |
| 5 |
| 15 |
| 4 |
| 9 |
| 4 |
| 15 |
| 4 |
| AE2+BE2 |
| 1 |
| 8 |
| 6 |
| 6 |
| 6 |
| 6 |
| 1 |
| 8 |


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
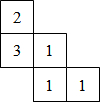 一个几何体由几块大小相同的小立方体达成,从上面观察这个几何体,看到的形状如图,其中小正方形中的数字表示在该位置小立方块的个数,请在下面相应的位置上画出这个几何体从正面、左面观察的形状图.
一个几何体由几块大小相同的小立方体达成,从上面观察这个几何体,看到的形状如图,其中小正方形中的数字表示在该位置小立方块的个数,请在下面相应的位置上画出这个几何体从正面、左面观察的形状图.查看答案和解析>>
科目:初中数学 来源: 题型:
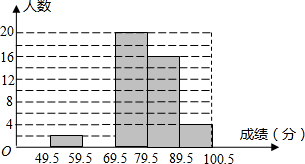 某校数学兴趣小组成员小华对本班上学期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析,绘制成频数分布直方图和频数、频率分布表.请你根据图表提供的信息,解答下列问题:
某校数学兴趣小组成员小华对本班上学期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析,绘制成频数分布直方图和频数、频率分布表.请你根据图表提供的信息,解答下列问题:| 分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合计 |
| 频数 | 2 | a | 20 | 16 | 4 | 50 |
| 频率 | 0.04 | 0.16 | 0.04 | 0.32 | b | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知△A′B′C′是由△ABC向上平移2个单位长度,再向右平移4个单位长度得到的,已知△ABC各顶点在平面直角坐标系中的坐标为:A(-1,0),B(3,-1),C(5,4).
已知△A′B′C′是由△ABC向上平移2个单位长度,再向右平移4个单位长度得到的,已知△ABC各顶点在平面直角坐标系中的坐标为:A(-1,0),B(3,-1),C(5,4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com