
����Ŀ����������ABC�У���D���߶�AB�ϣ�DE��BC��AC�ڵ�E����F��ֱ��BC�ϣ���ֱ��EF������D��ֱ��DH��AC��ֱ��EF�ڵ�H.
��1������ͼ1��ʾ������£���֤:��HDE=��C��
��2����������ABC���䣬D��E�����λ��Ҳ���䣬��F��ֱ��BC���˶�.
�ٵ���H��������ABC�ڲ�ʱ��ֱ��д����DHF���FEC��������ϵ��
�ڵ���H��������ABC�ⲿʱ�����н����Ƿ���Ȼ����������ͼ2�л�ͼ̽������˵������.
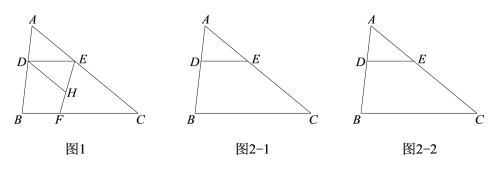
���𰸡���1��֤������������2���١�DHF����FEC=180�㣻�ڵ���H��������ABC�ⲿʱ����DHF=��FEC�����ɼ�����.
��������
��1�����ݡ�ƽ���ߵ����ʡ���ϡ���֪����������֤�����ɣ�
��2������ͼ1������H�ڡ�ABC�ڲ�ʱ����DH��AC�ɵ���FEC=��DHE�������DHE+��DHF=180�������ɵõ�����ʱ��DHF+��FEC=180�㣻
������H���ڡ�ABC�ڲ�ʱ���ֵ�H��ֱ��DE���Ϸ����·������������ͼ������ͼ2-1��ͼ2-2��ʾ���ٸ��ݡ�ƽ���ߵ����ʡ���ϡ���֪���������з���֤���ɵ�����ʱ��DHF=��FEC.
��1����DE��BC��
���ADE=��C��
��DH��AC��
���HDE=��ADE.
��2��������H�ڡ�ABC�ڲ�ʱ����DHF����FEC=180�㣬����������
��DH��AC��
���FEC=��DHE��
���ߡ�DHE+��DHF=180�㣬
����DHF+��FEC=180�㣻
�ڵ���H�ڡ�ABC�ⲿʱ�����н��۲�����������������
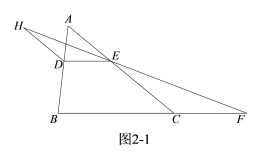
��).��ͼ2-1������H��ֱ��DE�Ϸ�ʱ��
��DH��AC��
���DHF=��FEC.
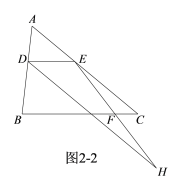
��).��ͼ2-2������H��ֱ��DE�·�ʱ��
��DH��AC��
���DHF=��FEC.
��������������H�ڡ�ABC�ⲿʱ����DHF=��FEC.


 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ƽ��ֱ������ϵ�У��ı���ABCD�dz����Σ���A=��B=��C=��D=90�㣬AB��CD��AB=CD=8cm��AD=BC=6cm��D����ԭ���غϣ�����Ϊ��0��0��
��1��д����B�����ꣻ
��2������P�ӵ�A������ÿ��3����λ���ȵ��ٶ����յ�B�����˶�������Q�ӵ�C������ÿ��4����λ���ȵ��ٶ�������CD���������˶�����P��Q����ͬʱ���������˶�ʱ��Ϊt����tΪ��ֵʱ��PQ��BC��
��3����Q�����й����У���Q�˶���ʲôλ��ʱ��ʹ��ADQ�����Ϊ9�����ʱQ������꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD�ı߳�Ϊ2��EΪBC�ߵ��ӳ�����һ�㣬CE��2������AE����CD���ڵ�F������BF���ӳ����߶�DE���ڵ�G����BG�ij�Ϊ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ʒ��������̨ʽ���Բ���ƽ����Բ����ֻ����ȣ�2018���ǰ����¸�Ʒ��ȫ����Ʒ���۶��600��Ԫ���±���ʾ��Ʒ����2018��ǰ����µ������۶ͳ����Ϣ��ȫ����ͼ1��ʾ��Ʒ���ֻ����������۶�ռ��Ʒ��������Ʒ�������۶�İٷֱ����ͳ��ͼ��
Ʒ�������۶�ͳ�Ʊ�����λ����Ԫ��
�·� | 1�� | 2�� | 3�� | 4�� | 5�� |
Ʒ�������۶� | 180 | 90 | 115 | 95 |

��![]() ����Ʒ��5�·ݵ����۶��� ��Ԫ��
����Ʒ��5�·ݵ����۶��� ��Ԫ��
��![]() ���ֻ���5�·ݵ����۶��� ��Ԫ��
���ֻ���5�·ݵ����۶��� ��Ԫ��
С��ͬѧ�۲�ͼ1����Ϊ���ֻ���5�·ݵ����۶���ֻ���4�·ݵ����۶�����ˣ���ͬ�����Ŀ�������˵�����ɣ�
��![]() ����Ʒ���ֻ�����A��B��C��D��E������ͣ�ͼ2��ʾ��5�·��ֻ������������۶�ռ5�·��ֻ������۶�İٷֱ����ͳ��ͼ����5�·� ���͵����۶���ߣ����۶���ߵĻ���ռ5�·ݸ�Ʒ�����۶�İٷֱ��� ��
����Ʒ���ֻ�����A��B��C��D��E������ͣ�ͼ2��ʾ��5�·��ֻ������������۶�ռ5�·��ֻ������۶�İٷֱ����ͳ��ͼ����5�·� ���͵����۶���ߣ����۶���ߵĻ���ռ5�·ݸ�Ʒ�����۶�İٷֱ��� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=8��AD=12������A��D����ġ�O��BC�������ڵ�E�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����н��ۣ�
����a��b��c��0����abc��0����![]() ��
��
����a��b��c��0����a��0����x��1һ���Ƿ���ax��b��c��0�Ľ⣻
����a��b��c��0����abc��0����abc��0��
����|a|>|b|����![]() >0.
>0.
������ȷ�Ľ�����(����)
A. �٢ڢ� B. �٢ڢ� C. �ڢۢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=x2+mx+n��ͼ����P����3��1�����Գ�����ֱ��x=��1��
��1����m��n��ֵ��
��2��xȡʲôֵʱ��y��x���������С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�O�У�ֱ��AB����CD�ڵ�G��CG=DG����O������BE��DO���ӳ����ڵ�E��F��DE���O�Ľ��㣬����BD��BF��
��1����֤����CDE=��E��
��2����OD=4��EF=1����CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
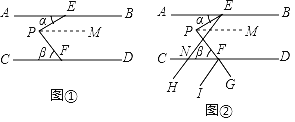
����Ŀ����ͼ�٣���֪AB��CD����E��F�ֱ���AB��CD�ϵĵ㣬��P����ƽ����֮���һ�㣬���AEP=������PFC=������ͼ���У�����E������EH��CD�ڵ�N��������FI���ӳ�PF��G��ʹ��PE��FG�ֱ�ƽ�֡�AEH����DFl���õ�ͼ����
��1����ͼ���У�����P��PM��AB������=20�㣬��=50��ʱ����EPM=�� ���ȣ���EPF=�� ���ȣ�
��2���ڣ�1���������£���ͼ���С�END���CFI�Ķ�����
��3����ͼ���У���FI��EHʱ����ֱ��д����������������ϵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com