
分析 分三种情况:
①AC=BC时,点C在AB的垂直平分线CM上,由直线CM的解析式为y=-4x+$\frac{11}{2}$,得出点C的坐标为($\frac{11}{8}$,0);
②当BC=AB=$\sqrt{17}$时,作BE⊥x轴于E,则CE=2$\sqrt{2}$,即可得出点C的坐标;
③当AC=AB=$\sqrt{17}$时,作AD⊥x轴于,则CD=4,即可得出点C的坐标;即可得出结果.
解答 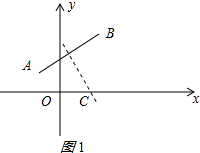 解:分三种情况:
解:分三种情况:
①AC=BC时,点C在AB的垂直平分线CM上,
如图1所示:
直线AB的解析式为y=$\frac{1}{4}$x+$\frac{5}{4}$,
那么直线CM的解析式为y=-4x+$\frac{11}{2}$,
当y=0时,x=$\frac{11}{8}$,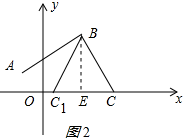 ∴点C的坐标为($\frac{11}{8}$,0);
∴点C的坐标为($\frac{11}{8}$,0);
②当BC=AB=$\sqrt{17}$时,作BE⊥x轴于E,如图2所示:
则CE=2$\sqrt{2}$,
∴点C的坐标为(3+2$\sqrt{2}$,0)或(3-2$\sqrt{2}$,0);
③当AC=AB=$\sqrt{17}$时,作AD⊥x轴于D,
如图3所示: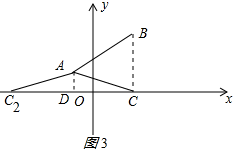 则CD=4,
则CD=4,
∴点C的坐标为(3,0)或(-5,0);
综上所述:点C的坐标为($\frac{11}{8}$,0)或(3+2$\sqrt{2}$,0)或(3-2$\sqrt{2}$,0)或(3,0)或(-5,0);
故答案为:($\frac{11}{8}$,0)或(3+2$\sqrt{2}$,0)或(-3+2$\sqrt{2}$,0)或(3,0)或(-5,0).
点评 本题考查了等腰三角形的判定、坐标与图形性质、勾股定理、直线解析式的求法等知识;本题综合性强,有一定难度,需要进行分类讨论才能得出结果.


科目:初中数学 来源: 题型:解答题
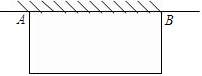 如图,某农户发展养禽业,准备利用现有的34米长的篱笆靠墙AB(墙长为25米)围成一个面积为120平方米的长方形养鸡场,这个养鸡场的长和宽各是多少?
如图,某农户发展养禽业,准备利用现有的34米长的篱笆靠墙AB(墙长为25米)围成一个面积为120平方米的长方形养鸡场,这个养鸡场的长和宽各是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
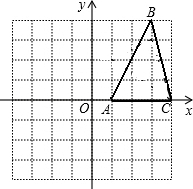 如图所示,每一个小方格都是边长为1的单位正方形.△ABC的三个顶点都在格点上,以点O为坐标原点建立平面直角坐标系.
如图所示,每一个小方格都是边长为1的单位正方形.△ABC的三个顶点都在格点上,以点O为坐标原点建立平面直角坐标系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com