
【题目】小华观察钟面(图1),了解到钟面上的分针每小时旋转360度,时针毎小时旋转30度.他为了进一步探究钟面上分针与时针的旋转规律,从下午2:00开始对钟面进行了一个小时的观察.为了探究方便,他将分针与分针起始位置OP(图2)的夹角记为y1 , 时针与OP的夹角记为y2度(夹角是指不大于平角的角),旋转时间记为t分钟.观察结束后,他利用获得的数据绘制成图象(图3),并求出y1与t的函数关系式: ![]() 请你完成:
请你完成: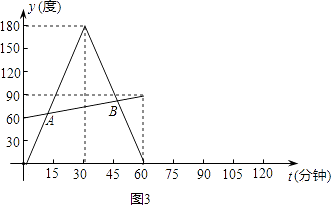

(1)求出图3中y2与t的函数关系式;
(2)直接写出A、B两点的坐标,并解释这两点的实际意义;
(3)若小华继续观察一个小时,请你在题图3中补全图象.
【答案】
(1)解:设y2与t的函数关系式为y2=kt+b,再把(0,60),(60,90)代入得: ![]() ,解得
,解得 ![]() ,
,
则解析式是:y=0.5t+60.
故y2与t的函数关系式为y2=0.5t+60
(2)解:A( ![]() ,
, ![]() ),B(
),B( ![]() ,
, ![]() );
);
当0≤t≤30时, ![]() ,解得
,解得  ;
;
当30<t≤60时, ![]() ,解得
,解得 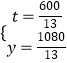 ,
,
故A( ![]() ,
, ![]() ),B(
),B( ![]() ,
, ![]() );
);
A表示时针与分针第一次重合的情况,B表示是经过 ![]() 分钟时针与分针关于OP成轴对称且与OP的夹角为
分钟时针与分针关于OP成轴对称且与OP的夹角为 ![]()
(3)解:

【解析】(1)设y2与t的函数关系式为y2=kt+b,再把(0,60),(60,90)代入此函数关系式即可求出k、b的值,进而得出结论;(2)求出两个函数的交点坐标即可;(3)分针会再转一圈,与第一个小时的情况相同,是一个循环,而时针OP的夹角增大的速度与第一个小时相同,即函数图象向右延伸.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:
【题目】计算下列各题
(1)计算:( ![]() )﹣2﹣6sin30°﹣(
)﹣2﹣6sin30°﹣( ![]() )0+
)0+ ![]() +|
+| ![]() ﹣
﹣ ![]() |
|
(2)化简:( ![]() ﹣
﹣ ![]() )÷
)÷ ![]() ,然后请自选一个你喜欢的x值,再求原式的值.
,然后请自选一个你喜欢的x值,再求原式的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,坐标平面上,二次函数y=﹣x2+4x﹣k的图形与x轴交于A,B两点,与y轴交于C点,其顶点为D,且k>0,若△ABC与△ABD的面积比为1:4,则k的值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°.将△ABC绕点A按逆时针方向旋转15°后得到△AB1C1 , B1C1交AC于点D,如果AD=2 ![]() ,则△ABC的周长等于 .
,则△ABC的周长等于 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解本校学生对球类运动的爱好情况,采用抽样的方法,从足球、篮球、排球、其它等四个方面调查了若干名学生,并绘制成“折线统计图”与“扇形统计图”.请你根据图中提供的部分信息解答下列问题: 

(1)在这次调查活动中,一共调查了名学生;
(2)“足球”所在扇形的圆心角是度;
(3)补全折线统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系XOY中,直线l1过点A(1,0)且与y轴平行,直线l2过点B(0,2)且与x轴平行,直线l1与直线l2相交于点P.点E为直线l2上一点,反比例函数 ![]() (k>0)的图象过点E与直线l1相交于点F.
(k>0)的图象过点E与直线l1相交于点F. 
(1)若点E与点P重合,求k的值;
(2)连接OE、OF、EF.若k>2,且△OEF的面积为△PEF的面积的2倍,求E点的坐标;
(3)是否存在点E及y轴上的点M,使得以点M、E、F为顶点的三角形与△PEF全等?若存在,求E点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点P是斜边AB的中点,点M从点C向点A匀速运动,点N从点B向点C匀速运动,已知两点同时出发,同时到达终点,连接PM、PN、MN,在整个运动过程中,△PMN的面积S与运动时间t的函数关系图象大致是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE.
(1)求证:四边形BCED′是平行四边形。
(2)若BE平分∠ABC,求证:AB2=AE2+BE2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com