
【题目】在平面直角坐标系XOY中,直线l1过点A(1,0)且与y轴平行,直线l2过点B(0,2)且与x轴平行,直线l1与直线l2相交于点P.点E为直线l2上一点,反比例函数 ![]() (k>0)的图象过点E与直线l1相交于点F.
(k>0)的图象过点E与直线l1相交于点F. 
(1)若点E与点P重合,求k的值;
(2)连接OE、OF、EF.若k>2,且△OEF的面积为△PEF的面积的2倍,求E点的坐标;
(3)是否存在点E及y轴上的点M,使得以点M、E、F为顶点的三角形与△PEF全等?若存在,求E点坐标;若不存在,请说明理由.
【答案】
(1)解:若点E与点P重合,则k=1×2=2
(2)解:当k>2时,如图1,
点E、F分别在P点的右侧和上方,过E作x轴的垂线EC,垂足为C,过F作y轴的垂线FD,垂足为D,EC和FD相交于点G,则四边形OCGD为矩形,
∵PF⊥PE,
∴S△FPE= ![]() PEPF=
PEPF= ![]() (
( ![]() ﹣1)(k﹣2)=
﹣1)(k﹣2)= ![]() k2﹣k+1,
k2﹣k+1,
∴四边形PFGE是矩形,
∴S△PFE=S△GEF,
∴S△OEF=S矩形OCGD﹣S△DOF﹣S△EGF﹣S△OCE= ![]() k﹣
k﹣ ![]() ﹣(
﹣( ![]() k2﹣k+1)﹣
k2﹣k+1)﹣ ![]() =
= ![]() k2﹣1,
k2﹣1,
∵S△OEF=2S△PEF,
∴ ![]() k2﹣1=2(
k2﹣1=2( ![]() k2﹣k+1),
k2﹣k+1),
解得k=6或k=2,
∵k=2时,E、F重合,
∴k=6,
∴E点坐标为:(3,2)

(3)解:存在点E及y轴上的点M,使得△MEF≌△PEF,
①当k<2时,如图2,只可能是△MEF≌△PEF,作FH⊥y轴于H,

∵∠MHF=∠EBM=90°,∠HMF=∠MEB,
∴△FHM∽△MBE,
∴ ![]() ,
,
∵FH=1,EM=PE=1﹣ ![]() ,FM=PF=2﹣k,
,FM=PF=2﹣k,
∴ ![]() =
= ![]() ,BM=
,BM= ![]() ,
,
在Rt△MBE中,由勾股定理得,EM2=EB2+MB2,
∴(1﹣ ![]() )2=(
)2=( ![]() )2+(
)2+( ![]() )2,
)2,
解得k= ![]() ,此时E点坐标为(
,此时E点坐标为( ![]() ,2),
,2),
②当k>2时,如图3,

只可能是△MFE≌△PEF,作FQ⊥y轴于Q,△FQM∽△MBE得, ![]() ,
,
∵FQ=1,EM=PF=k﹣2,FM=PE= ![]() ﹣1,
﹣1,
∴ ![]() =
= ![]() ,BM=2,
,BM=2,
在Rt△MBE中,由勾股定理得,EM2=EB2+MB2,
∴(k﹣2)2=( ![]() )2+22,解得k=
)2+22,解得k= ![]() 或0,但k=0不符合题意,
或0,但k=0不符合题意,
∴k= ![]() .
.
此时E点坐标为( ![]() ,2),
,2),
∴符合条件的E点坐标为( ![]() ,2)(
,2)( ![]() ,2).
,2).
【解析】(1)根据反比例函数中k=xy进行解答即可;(2)当k>2时,点E、F分别在P点的右侧和上方,过E作x轴的垂线EC,垂足为C,过F作y轴的垂线FD,垂足为D,EC和FD相交于点G,则四边形OCGD为矩形,再求出S△FPE= ![]() k2﹣k+1,根据S△OEF=S矩形OCGD﹣S△DOF﹣S△EGF﹣S△OCE即可求出k的值,进而求出E点坐标;(3)①当k<2时,只可能是△MEF≌△PEF,作FH⊥y轴于H,由△FHM∽△MBE可求出BM的值,再在Rt△MBE中,由勾股定理得,EM2=EB2+MB2 , 求出k的值,进而可得出E点坐标; ②当k>2时,只可能是△MFE≌△PEF,作FQ⊥y轴于Q,△FQM∽△MBE得,
k2﹣k+1,根据S△OEF=S矩形OCGD﹣S△DOF﹣S△EGF﹣S△OCE即可求出k的值,进而求出E点坐标;(3)①当k<2时,只可能是△MEF≌△PEF,作FH⊥y轴于H,由△FHM∽△MBE可求出BM的值,再在Rt△MBE中,由勾股定理得,EM2=EB2+MB2 , 求出k的值,进而可得出E点坐标; ②当k>2时,只可能是△MFE≌△PEF,作FQ⊥y轴于Q,△FQM∽△MBE得, ![]() ,可求出BM的值,再在Rt△MBE中,由勾股定理得,EM2=EB2+MB2 , 求出k的值,进而可得出E点坐标.
,可求出BM的值,再在Rt△MBE中,由勾股定理得,EM2=EB2+MB2 , 求出k的值,进而可得出E点坐标.
【考点精析】掌握勾股定理的概念和相似三角形的判定与性质是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.当飞机到达距离海面3000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣ ![]() x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华观察钟面(图1),了解到钟面上的分针每小时旋转360度,时针毎小时旋转30度.他为了进一步探究钟面上分针与时针的旋转规律,从下午2:00开始对钟面进行了一个小时的观察.为了探究方便,他将分针与分针起始位置OP(图2)的夹角记为y1 , 时针与OP的夹角记为y2度(夹角是指不大于平角的角),旋转时间记为t分钟.观察结束后,他利用获得的数据绘制成图象(图3),并求出y1与t的函数关系式: ![]() 请你完成:
请你完成: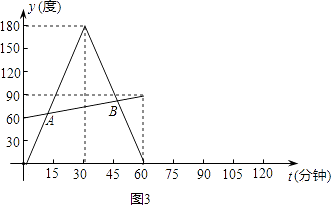

(1)求出图3中y2与t的函数关系式;
(2)直接写出A、B两点的坐标,并解释这两点的实际意义;
(3)若小华继续观察一个小时,请你在题图3中补全图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为 米(结果精确到0.1米,参考数据:![]() =1.41,
=1.41,![]() =1.73).
=1.73).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校申报“跳绳特色运动”学校一年后,抽样调查了部分学生的“1分钟跳绳”成绩,并制成了下面的频数分布直方图(每小组含最小值,不含最大值)和扇形图.
(1)补全频数分布直方图,扇形图中m= ;
(2)若把每组中各个数据用这组数据的中间值代替(如A组80≤x<100的中间值是![]() =90次),则这次调查的样本平均数是多少?
=90次),则这次调查的样本平均数是多少?
(3)如果“1分钟跳绳”成绩大于或等于120次为优秀,那么该校2100名学生中“1分钟跳绳”成绩为优秀的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⊙O为△ABC的外接圆,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法).
(1)如图1,AC=BC
(2)如图2,直线l与⊙O相切于点P,且l∥BC。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的MN这层上晒太阳.(![]() 取1.73)
取1.73)
(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com