
【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的MN这层上晒太阳.(![]() 取1.73)
取1.73)
(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.
【答案】
(1)
解:当α=60°时,在Rt△ABE中,
∵tan60°=![]() =
=![]() ,
,
∴AB=10tan60°=10![]() ≈10×1.73=17.3米.
≈10×1.73=17.3米.
即楼房的高度约为17.3米
(2)
解:当α=45°时,小猫仍可以晒到太阳.理由如下:
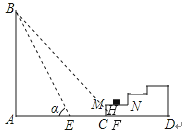
假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为点F,与MC的交点为点H.
∵∠BFA=45°,
∴tan45°=![]() =1,
=1,
此时的影长AF=AB=17.3米,
∴CF=AF﹣AC=17.3﹣17.2=0.1米,
∴CH=CF=0.1米,
∴大楼的影子落在台阶MC这个侧面上,
∴小猫仍可以晒到太阳.
【解析】(1)在Rt△ABE中,由tan60°=![]() =
=![]() ,即可求出AB=10tan60°=17.3米;
,即可求出AB=10tan60°=17.3米;
(2)假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为点F,与MC的交点为点H.由∠BFA=45°,可得AF=AB=17.3米,那么CF=AF﹣AC=0.1米,CH=CF=0.1米,所以大楼的影子落在台阶MC这个侧面上,故小猫仍可以晒到太阳.
此题考查了解直角三角形中光线形成的角度与影长的问题,通过解直角三角形利用三角函数解答问题。


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系XOY中,直线l1过点A(1,0)且与y轴平行,直线l2过点B(0,2)且与x轴平行,直线l1与直线l2相交于点P.点E为直线l2上一点,反比例函数 ![]() (k>0)的图象过点E与直线l1相交于点F.
(k>0)的图象过点E与直线l1相交于点F. 
(1)若点E与点P重合,求k的值;
(2)连接OE、OF、EF.若k>2,且△OEF的面积为△PEF的面积的2倍,求E点的坐标;
(3)是否存在点E及y轴上的点M,使得以点M、E、F为顶点的三角形与△PEF全等?若存在,求E点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=3cm.BC=2cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1 , 连接AC1 , BD1 . 如果四边形ABD1C1是矩形,那么平移的距离为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE.
(1)求证:四边形BCED′是平行四边形。
(2)若BE平分∠ABC,求证:AB2=AE2+BE2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形 OABC中,OA=3,OC=5,分别以 OA、OC所在直线为x 轴、y 轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数y=![]() (k>0)的图象经过点D且与边BA交于点E,连接DE.
(k>0)的图象经过点D且与边BA交于点E,连接DE.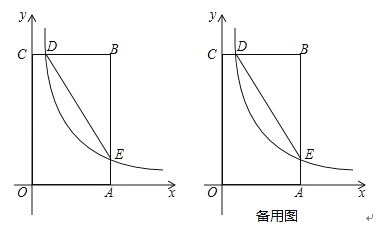
(1)连接OE,若△EOA的面积为2,则k=
(2)连接CA,DE与CA是否平行?请说明理由:
(3)是否存在点D,使得点B关于DE的对称点在OC上?若存在,求出点D的坐标;若不存在,请说明理由:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,4) 
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1 , 直接写出点A1的坐标;
(2)请画出△ABC绕原点O顺时针旋转90°的图形△A2B2C2 , 直接写出点A2的坐标;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com