
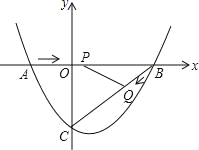
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx-3��a��0����x�ύ�ڵ�A��-2��0����B��4��0�����㣬��y�ύ�ڵ�C��
��1���������ߵĽ���ʽ��
��2����P��A����������߶�AB����ÿ��3����λ���ȵ��ٶ���B���˶���ͬʱ��Q��B����������߶�BC����ÿ��1����λ���ȵ��ٶ���C���˶�������һ���㵽���յ�ʱ����һ����Ҳֹͣ�˶�������PBQ����ʱ�����˶�������ʹ��PBQ���������������Ƕ��٣�
��3������PBQ��������ʱ����BC�·����������ϴ��ڵ�K��ʹS��CBK��S��PBQ=5��2����K�����꣮
���𰸡�(1) y=![]() x2-
x2-![]() x-3��(2) �˶�1��ʹ��PBQ����������������
x-3��(2) �˶�1��ʹ��PBQ����������������![]() ����3��K1��1��-
����3��K1��1��-![]() ����K2��3��-
����K2��3��-![]() ����
����
��������
�����������1���ѵ�A��B������ֱ���������߽���ʽ���г�����ϵ��a��b�Ľ���ʽ��ͨ���ⷽ����������ǵ�ֵ��
��2�����˶�ʱ��Ϊt�룮���������ε������ʽ�г�S��PBQ��t�ĺ�����ϵʽS��PBQ=-![]() ��t-1��2+
��t-1��2+![]() �����ö��κ�����ͼ�����ʽ��н��
�����ö��κ�����ͼ�����ʽ��н��
��3�����ô���ϵ�������ֱ��BC�Ľ���ʽΪy=![]() x-3���ɶ��κ���ͼ���ϵ���������������K������Ϊ��m��
x-3���ɶ��κ���ͼ���ϵ���������������K������Ϊ��m��![]() m2-
m2-![]() m-3����
m-3����
��ͼ2������K��KE��y�ᣬ��BC�ڵ�E�������֪�����ͣ�2���еĽ�����S��CBK=![]() �������ͼ�εõ���S��CBK=S��CEK+S��BEK=
�������ͼ�εõ���S��CBK=S��CEK+S��BEK=![]() EKm+
EKm+![]() EK��4-m����������߶εij��ȴ�����֪��-
EK��4-m����������߶εij��ȴ�����֪��-![]() m2+3m=
m2+3m=![]() �������K1��1��-
�������K1��1��-![]() ����K2��3��-
����K2��3��-![]() ����
����
�����������1���ѵ�A��-2��0����B��4��0���ֱ����y=ax2+bx-3��a��0������
![]() ��
��
���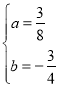 ��
��
���Ը������ߵĽ���ʽΪ��y=![]() x2-
x2-![]() x-3��
x-3��
��2�����˶�ʱ��Ϊt�룬��AP=3t��BQ=t��
��PB=6-3t��
������ã���C������Ϊ��0��-3����
��Rt��BOC��BC=![]() =5��
=5��
��ͼ1������Q��QH��AB�ڵ�H��
��QH��CO��
���BHQ�ס�BOC��
��![]() ����
����![]() ��
��
��HQ=![]() t��
t��
��S��PBQ=![]() PBHQ=
PBHQ=![]() ��6-3t��
��6-3t��![]() t=-
t=-![]() t2+
t2+![]() t=-
t=-![]() ��t-1��2+
��t-1��2+![]() ��
��
����PBQ����ʱ��0��t��2
�൱t=1ʱ��
S��PBQ���=![]() ��
��
���˶�1��ʹ��PBQ����������������![]() ��
��
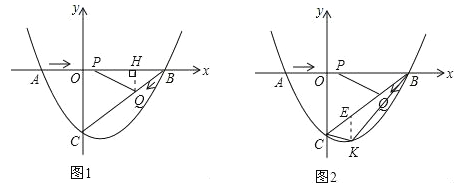
��3����ֱ��BC�Ľ���ʽΪy=kx+c��k��0����
��B��4��0����C��0��-3�����룬��
![]() ��
��
���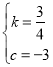 ��
��
��ֱ��BC�Ľ���ʽΪy=![]() x-3��
x-3��
�ߵ�K���������ϣ�
�����K��������m��![]() m2-
m2-![]() m-3����
m-3����
��ͼ2������K��KE��y�ᣬ��BC�ڵ�E�����E������Ϊ��m��![]() m-3����
m-3����
��EK=![]() m-3-��
m-3-��![]() m2-
m2-![]() m-3��=-
m-3��=-![]() m2+
m2+![]() m��
m��
����PBQ��������ʱ����S��CBK��S��PBQ=5��2��S��PBQ=![]() ��
��
��S��CBK=![]() ��
��
S��CBK=S��CEK+S��BEK=![]() EKm+
EKm+![]() EK��4-m��
EK��4-m��
=![]() ��4EK
��4EK
=2��-![]() m2+
m2+![]() m��
m��
=-![]() m2+3m��
m2+3m��
����-![]() m2+3m=
m2+3m=![]() ��
��
��� m1=1��m2=3��
��K1��1��-![]() ����K2��3��-
����K2��3��-![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A��4��0����B��0��4![]() ������һ��ֱ�����dz�DEF���ڡ�OAB�ڣ�ʹ��б��FD���߶�AB�ϣ����dz߿������߶�AB���»��������С�EFD=30�㣬ED=2����GΪ��FD���е㣮
������һ��ֱ�����dz�DEF���ڡ�OAB�ڣ�ʹ��б��FD���߶�AB�ϣ����dz߿������߶�AB���»��������С�EFD=30�㣬ED=2����GΪ��FD���е㣮
��1����ֱ��AB�Ľ���ʽ��
��2����ͼ1������D���A�غ�ʱ������G�ķ���������y=![]() ��k��0���Ľ���ʽ��
��k��0���Ľ���ʽ��
��3�������dz����Ĺ����У�������G�ķ�����������ͼ���ܷ�ͬʱ������F������ܣ������ʱ�����������Ľ���ʽ��������ܣ�˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��y=��x��2���������� ��
A����һ���� B���ڶ����� C���������� D����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=-1���������߾���A��1��0����C��0��3�����㣬��x�ύ�ڵ�B��
��1����ֱ��y=mx+n����B��C���㣬��ֱ��BC�������ߵĽ���ʽ��
��2���������ߵĶԳ���x=-1����һ��M��ʹ��M����A�ľ����뵽��C�ľ���֮����С�������M�����ꣻ
��3�����PΪ�����ߵĶԳ���x=-1�ϵ�һ�����㣬��ʹ��BPCΪֱ�������εĵ�P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����з�����һԪһ�η��̵��ǣ�������
A. x��2��3 B. 1��5��6 C. x2��x��1 D. x��3y��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ɽ�����г�Խ��Խ�ܵ���ѧ����ϲ��������Ʒ�����Ͷ���г���ij���о�Ӫ��A�ͳ�ȥ�������ܶ�Ϊ5��Ԫ������ÿ�����ۼ۱�ȥ�꽵��400Ԫ����������������ͬ�������ܶ��ȥ�����20%��
��1������A�ͳ�ÿ���ۼ۶���Ԫ�������з��̵ķ������
��2���ó��мƻ��½�һ��A�ͳ����¿�B�ͳ���60������B�ͳ��Ľ�������������A�ͳ�������������Ӧ��ν�������ʹ������������ࣿ
A��B�����ͺų��Ľ��������ۼ۸����±���
A�ͳ� | B�ͳ� | |
�����۸�Ԫ�� | 1100 | 1400 |
���ۼ۸�Ԫ�� | ��������ۼ۸� | 2000 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ�������
A. ������һö�ʵؾ��ȵ�Ӳ��10�Σ�һ����5����������
B. ����Ԥ��˵������Ľ�ˮ����Ϊ40%������ʾ������40%��ʱ�䶼�ڽ���
C. �������Ա�ڷ�������Ͷ��һ�Σ�Ͷ����Ϊ����¼�
D. ��a��ʵ����|a|��0���Dz������¼�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
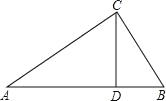
����Ŀ����ͼ����ABC�У�CD�DZ�AB�ϵĸߣ���![]() ��
��
��1����֤����ACD�ס�CBD��
��2�����ACB�Ĵ�С��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com