练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

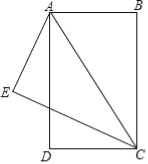
    【题目】如图，已知BA=AE=DC，AD=EC，CE⊥AE，垂足为E．

    （1）求证：△DCA≌△EAC；

    （2）只需添加一个条件，即 ，可使四边形ABCD为矩形．请加以证明．

    【答案】(1)详见解析；(2)AD=BC（答案不唯一）．

    【解析】试题分析：（1）由SSS证明△DCA≌△EAC即可；（2）先证明四边形ABCD是平行四边形，再由全等三角形的性质得出∠D=90°，即可得出结论．

    试题解析：

    （1）证明：在△DCA和△EAC中，，

    ∴△DCA≌△EAC（SSS）；

    （2）添加AD=BC，可使四边形ABCD为矩形；理由如下：

    ∵AB=DC，AD=BC，

    ∴四边形ABCD是平行四边形，

    ∵CE⊥AE，

    ∴∠E=90°，

    由（1）得：△DCA≌△EAC，

    ∴∠D=∠E=90°，

    ∴四边形ABCD为矩形；

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为保护环境，我市公交公司计划购买A型和B型两种环保节能公交车共10辆．若购买A型公交车1辆，B型公交车2辆，共需400万元；若购买A型公交车2辆，B型公交车1辆，共需350万元．

    （1）求购买A型和B型公交车每辆各需多少万元？

    （2）预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次．若该公司购买A型和B型公交车的总费用不超过1200万元，且确保这10辆公交车在该线路的年均载客总和不少于680万人次，则该公司有哪几种购车方案？

    （3）在（2）的条件下，哪种购车方案总费用最少？最少总费用是多少万元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学决定改变办学条件计划拆除一部分旧校舍、建造新校舍．计划在年内拆除旧校舍与建造新校

    舍共5000平方米，在实施中为扩大绿化面积，新建校舍只完成了计划的70％，而拆除校舍则超过计划

    的20％，结果拆、建的总面积恰好为5000平方米．

    （1）求原计划拆、建的面积各多少平方米？

    （2）若拆除旧校舍每平米需100元，建造新校舍每平米需500元．求实际拆、建的费用共多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学开展了“手机伴我健康行”主题活动．他们随机抽取部分学生进行“手机使用目的”和“每周使用手机时间”的问卷调查，并绘制成如图①②的统计图。已知“查资料”人人数是40人。

    请你根据以上信息解答以下问题

    （1）在扇形统计图中，“玩游戏”对应的圆心角度数是_______________。

    （2）补全条形统计图

    （3）该校共有学生1200人，估计每周使用手机时间在2小时以上（不含2小时）的人数

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学改革学生的学习模式，变“老师要学生学习”为“学生自主学习”，培养了学生自主学习的能力．小华与小明同学就“你最喜欢哪种学习方式”随机调查了他们周围的一些同学，根据收集到的数据绘制了以下两个不完整的统计图（如图）．

    请根据上面两个不完整的统计图回答以下4个问题：

    （1）这次抽样调查中，共调查了_____名学生．

    （2）补全条形统计图中的缺项．

    （3）在扇形统计图中，选择教师传授的占_____%，选择小组合作学习的占_____%．

    （4）根据调查结果，估算该校1800名学生中大约有_____人选择小组合作学习模式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=-x2+x- ，当自变量x取m时对应的值大于0，当自变量x分别取m-1、m+1时对应的函数值为y1、y2 ， 则y1、y2必须满足（　　）
    A.y1＞0、y2＞0
    B.y1＜0、y2＜0
    C.y1＜0、y2＞0
    D.y1＞0、y2＜0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】八(2)班组织了一次经典诵读比赛，甲、乙两队各10人的比赛成绩如下表(10分制)：

    甲

    7

    8

    9

    7

    10

    10

    9

    10

    10

    10

    乙

    10

    8

    7

    9

    8

    10

    10

    9

    10

    9

    (1)甲队成绩的中位数是 分，乙队成绩的众数是 分；

    (2)计算乙队的平均成绩和方差；

    (3)已知甲队成绩的方差是1.4，则成绩较为整齐的是 队．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在 中， ， ，将 绕点O沿逆时针方向旋转 得到 ，连结 ，求证：四边形 是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，□ABCD的对角线AC、BD相交于点O，EF过点O且与AB、CD分别相交于点E、F，连接EC．

    （1）求证：OE＝OF；

    （2）若EF⊥AC，△BEC的周长是10，求□ABCD的周长．

    查看答案和解析>>

    同步练习册答案