
【题目】如图,在 ![]() 中,
中, ![]() ,
, ![]() ,将
,将 ![]() 绕点O沿逆时针方向旋转
绕点O沿逆时针方向旋转 ![]() 得到
得到 ![]() ,连结
,连结 ![]() ,求证:四边形
,求证:四边形 ![]() 是平行四边形.
是平行四边形.
【答案】证明:∵在 ![]() 中,
中, ![]() ,
, ![]() ,∴
,∴ ![]() ,结合图形旋转的性质可知:
,结合图形旋转的性质可知: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,∴
,∴ ![]() ,∵
,∵ ![]() ,∴四边形
,∴四边形 ![]() 是平行四边形.
是平行四边形.
【解析】可以根据四边形的一组对边平行且相等来判定四边形为平行四边形.
【考点精析】利用平行四边形的判定和图形的旋转对题目进行判断即可得到答案,需要熟知两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.旋转的方向、角度、旋转中心是它的三要素.


科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用.
(1)如图1可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)比较图1、图2两图的阴影部分面积,可以得到
乘法公式 (用式子表达);
(3)运用你所得到的公式,计算下列各题:
①(2m+n﹣p)(2m﹣n+p) ②10.3×9.7.

查看答案和解析>>
科目:初中数学 来源: 题型:
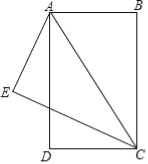
【题目】如图,已知BA=AE=DC,AD=EC,CE⊥AE,垂足为E.
(1)求证:△DCA≌△EAC;
(2)只需添加一个条件,即 ,可使四边形ABCD为矩形.请加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在△ABC中,∠BAC=2∠B,∠BAD=∠DAC.说明:∠BAD=∠B.
(2)如图2,已知点E在BA延长线上,∠EAD=∠CAD,∠B=∠C.说明:AD∥BC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y= ![]() (x-1)2-3 .
(x-1)2-3 .
(1)写出抛物线的开口方向、对称轴;
(2)函数y有最大值还是最小值?并求出这个最大(小)值;
(3)设抛物线与y轴的交点为P,与x轴的交点为Q,求直线PQ的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,直线AB∥CD
(1)如图1,点E在直线BD的左侧,猜想∠ABE、∠CDE、∠BED的数量关系,并证明你的结论;
(2)如图2,点E在直线BD的左侧,BF、DF分别平分∠ABE、∠CDE,猜想∠BFD和∠BED的数量关系,并证明你的结论;
(3)如图3,点E在直线BD的右侧,BF、DF分别平分∠ABE、∠CDE;那么第(2)题中∠BFD和∠BED的数量关系的猜想是否仍成立?如果成立,请证明;如果不成立,请写出你的猜想,并证明.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,∠AOB=90°,点C在射线OA上,CD∥OE.
(1)如图1,若∠OCD=120°,求∠BOE的度数;
(2)把“∠AOB=90°”改为“∠AOB=120°”,射线OE沿射线OB平移,得O′E,其他条件不变,(如图2所示),探究∠OCD、∠BO′E的数量关系;
(3)在(2)的条件下,作PO′⊥OB垂足为O′,与∠OCD的平分线CP交于点P,若∠BO′E=α,请用含α的式子表示∠CPO′(请直接写出答案).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com