Question

【题目】已知：抛物线y= (x-1)2-3 ．
（1）写出抛物线的开口方向、对称轴；
（2）函数y有最大值还是最小值？并求出这个最大（小）值；
（3）设抛物线与y轴的交点为P，与x轴的交点为Q，求直线PQ的函数解析式．

Answer 1

【答案】
（1）

解：抛物线y= (x-1)2-3，

∵a= ＞0，

∴抛物线的开口向上，对称轴为直线x=1；

（2）

解：∵a= ＞0，

∴函数y有最小值，最小值为-3；

（3）

解：令x=0，则y= (0-1)2-3=- ，所以，点P的坐标为（0，- ），令y=0，则 (x-1)2-3=0，

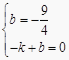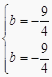解得x1=-1，x2=3，所以，点Q的坐标为（-1，0）或（3，0），当点P（0，- ），Q（-1，0）时，设直线PQ的解析式为y=kx+b，则， ，解得 ，所以直线PQ的解析式为y=- x- ，

当P（0，- ），Q（3，0）时，设直线PQ的解析式为y=mx+n，

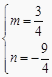则 ，解得 ，所以，直线PQ的解析式为y= x- ，综上所述，直线PQ的解析式为y=- x- 或y= x- .

【解析】（1）根据二次函数的性质，写出开口方向与对称轴即可；（2）根据a是正数确定有最小值，再根据函数解析式写出最小值；（3）分别求出点P、Q的坐标，再根据待定系数法求函数解析式解答．
【考点精析】利用二次函数的性质和二次函数的最值对题目进行判断即可得到答案，需要熟知增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小；如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a．