
【题目】如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确的个数是( )
①AE=BF;②AE⊥BF;③sin∠BQP= ![]() ;④S四边形ECFG=2S△BGE .
;④S四边形ECFG=2S△BGE . 
A.4
B.3
C.2
D.1
【答案】B
【解析】解:∵E,F分别是正方形ABCD边BC,CD的中点,
∴CF=BE,
在△ABE和△BCF中, ,
,
∴Rt△ABE≌Rt△BCF(SAS),
∴∠BAE=∠CBF,AE=BF,故①正确;
又∵∠BAE+∠BEA=90°,
∴∠CBF+∠BEA=90°,
∴∠BGE=90°,
∴AE⊥BF,故②正确;
根据题意得,FP=FC,∠PFB=∠BFC,∠FPB=90°
∵CD∥AB,
∴∠CFB=∠ABF,
∴∠ABF=∠PFB,
∴QF=QB,
令PF=k(k>0),则PB=2k
在Rt△BPQ中,设QB=x,
∴x2=(x﹣k)2+4k2 ,
∴x= ![]() ,
,
∴sin=∠BQP= ![]() =
= ![]() ,故③正确;
,故③正确;
∵∠BGE=∠BCF,∠GBE=∠CBF,
∴△BGE∽△BCF,
∵BE= ![]() BC,BF=
BC,BF= ![]() BC,
BC,
∴BE:BF=1: ![]() ,
,
∴△BGE的面积:△BCF的面积=1:5,
∴S四边形ECFG=4S△BGE , 故④错误.
故选:B.
首先证明△ABE≌△BCF,再利用角的关系求得∠BGE=90°,即可得到①AE=BF;②AE⊥BF;△BCF沿BF对折,得到△BPF,利用角的关系求出QF=QB,解出BP,QB,根据正弦的定义即可求解;根据AA可证△BGE与△BCF相似,进一步得到相似比,再根据相似三角形的性质即可求解.本题主要考查了四边形的综合题,涉及正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质以及折叠的性质的知识点,解决的关键是明确三角形翻转后边的大小不变,找准对应边,角的关系求解.


科目:初中数学 来源: 题型:
【题目】已知:抛物线y= ![]() (x-1)2-3 .
(x-1)2-3 .
(1)写出抛物线的开口方向、对称轴;
(2)函数y有最大值还是最小值?并求出这个最大(小)值;
(3)设抛物线与y轴的交点为P,与x轴的交点为Q,求直线PQ的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.
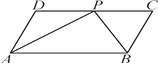
(1)求∠APB的度数;
(2)如果AD=5 cm,AP=8 cm,求△APB的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形的顶点A(1,1)、B(3,1),规定把等边△ABC“先沿x轴翻折,再向左平移1个单位”为一次変换,如果这样连续经过2016次变换后,等边△ABC的顶点C的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
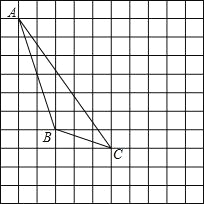
【题目】如图,每个小正方形的边长为 1 个单位,每个小方格的顶点叫格点.
(1)画出△ABC 的 AB 边上的中线 CD;
(2)画出△ABC 向右平移 4 个单位后得到的△A1B1C1;
(3)图中 AC 与 A1C1 的关系是: ;
(4)图中△ABC 的面积是 ;
(5)能使△BCE 面积为 3 的格点 E 有 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,∠AOB=90°,点C在射线OA上,CD∥OE.
(1)如图1,若∠OCD=120°,求∠BOE的度数;
(2)把“∠AOB=90°”改为“∠AOB=120°”,射线OE沿射线OB平移,得O′E,其他条件不变,(如图2所示),探究∠OCD、∠BO′E的数量关系;
(3)在(2)的条件下,作PO′⊥OB垂足为O′,与∠OCD的平分线CP交于点P,若∠BO′E=α,请用含α的式子表示∠CPO′(请直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A城出发前往B城,在整个行程中,两车离开A城的距离y与t的对应关系如图所示:
(1)A、B两城之间距离是多少千米?
(2)求乙车出发多长时间追上甲车?
(3)直接写出甲车出发多长时间,两车相距20千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com