
【题目】如图,四边形ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.
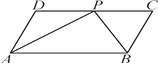
(1)求∠APB的度数;
(2)如果AD=5 cm,AP=8 cm,求△APB的周长.
【答案】(1)∠APB=90°; (2)△APB的周长是24cm.
【解析】试题分析:(1)根据平行四边形性质得出AD∥CB,AB∥CD,推出∠DAB+∠CBA=180°,求出∠PAB+∠PBA=90°,在△APB中求出∠APB即可;
(2)求出AD=DP=5,BC=PC=5,求出DC=10=AB,即可求出答案.
解:(1)∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA=![]() (∠DAB+∠CBA)=90°,
(∠DAB+∠CBA)=90°,
在△APB中,
∴∠APB=180°﹣(∠PAB+∠PBA)=90°;
(2)∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵AB∥CD,
∴∠PAB=∠DPA
∴∠DAP=∠DPA
∴△ADP是等腰三角形,
∴AD=DP=5cm
同理:PC=CB=5cm
即AB=DC=DP+PC=10cm,
在Rt△APB中,AB=10cm,AP=8cm,
∴BP=![]() =6(cm)
=6(cm)
∴△APB的周长是6+8+10=24(cm).


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】某中学改革学生的学习模式,变“老师要学生学习”为“学生自主学习”,培养了学生自主学习的能力.小华与小明同学就“你最喜欢哪种学习方式”随机调查了他们周围的一些同学,根据收集到的数据绘制了以下两个不完整的统计图(如图).


请根据上面两个不完整的统计图回答以下4个问题:
(1)这次抽样调查中,共调查了_____名学生.
(2)补全条形统计图中的缺项.
(3)在扇形统计图中,选择教师传授的占_____%,选择小组合作学习的占_____%.
(4)根据调查结果,估算该校1800名学生中大约有_____人选择小组合作学习模式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的菱形ABCD中,∠A=60°,点M是AD边的中点,连接MC,将菱形ABCD翻折,使点A落在线段CM上的点E处,折痕交AB于点N,则线段EC的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县各中小学校积极组织学生开展课外阅读活动,为了解某校学生每周课外阅读的时间量t(单位:小时),采用随机抽样的方法抽取部分学生进行了问卷调查,调查结果按0≤t〈2,2≤t〈3,3≤t〈4,t≥4分为四个等级,并分别用A、B、C、D表示.根据调查结果统计数据绘制成如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:
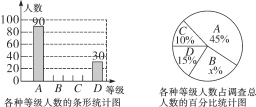
(1)求这次抽查的学生总数是多少人,并求出x的值;
(2)将不完整的条形统计图补充完整;
(3)若该校共有学生3600人,试估计每周课外阅读时间量满足2≤t〈4的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD的对角线AC、BD相交于点O,EF过点O且与AB、CD分别相交于点E、F,连接EC.
(1)求证:OE=OF;
(2)若EF⊥AC,△BEC的周长是10,求□ABCD的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发门市销售两种商品,甲种商品每件售价为300元,乙种商品每件售价为80元.新年来临之际,该门市为促销制定了两种优惠方案:
方案一:买一件甲种商品就赠送一件乙种商品;
方案二:按购买金额打八折付款.
某公司为奖励员工,购买了甲种商品20件,乙种商品x(x≥20)件.
(1)分别写出优惠方案一购买费用y1(元)、优惠方案二购买费用y2(元)与所买乙种商品x(件)之间的函数关系式;
(2)若该公司共需要甲种商品20件,乙种商品40件.设按照方案一的优惠办法购买了m件甲种商品,其余按方案二的优惠办法购买.请你写出总费用w与m之间的关系式;利用w与m之间的关系式说明怎样购买最实惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确的个数是( )
①AE=BF;②AE⊥BF;③sin∠BQP= ![]() ;④S四边形ECFG=2S△BGE .
;④S四边形ECFG=2S△BGE . 
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,矩形ABCD中,AB=2,BC=5,E、P分别在AD、BC上,且DE=BP=1.
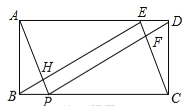
(1)断⊿BEC的形状,并说明理由;
(2)判断四边形EFPH是什么特殊四边形?并证明你的判断。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com