
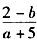 ?为什么?反之能否从x=
?为什么?反之能否从x=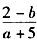 得到x(a+5)=2-b?为什么?
得到x(a+5)=2-b?为什么? 科目:初中数学 来源: 题型:
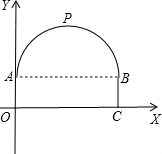 中央且距地面6m,建立如图所示的坐标系:
中央且距地面6m,建立如图所示的坐标系:查看答案和解析>>
科目:初中数学 来源: 题型:
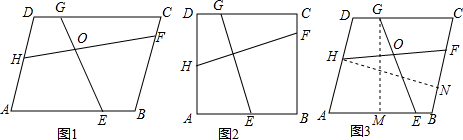
| EG |
| FH |
| b |
| a |
| EG |
| FH |
| b |
| a |
查看答案和解析>>
科目:初中数学 来源: 题型:
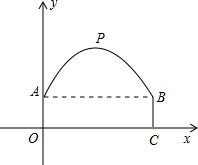 一座隧道的截面由抛物线和长方形构成,长方形的长为8m,宽为2m,隧道最高点P位于AB的中央且距地面6m,建立如图所示的坐标系.
一座隧道的截面由抛物线和长方形构成,长方形的长为8m,宽为2m,隧道最高点P位于AB的中央且距地面6m,建立如图所示的坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,从一个边长为1米的正方形铁皮中剪下一个扇形.
如图,从一个边长为1米的正方形铁皮中剪下一个扇形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com