Question

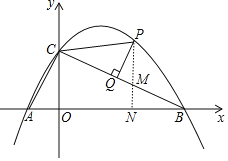
【题目】如图，二次函数的图像与轴交于点A、B，与轴交于点C．

（1） ； ；

（2）点P为该函数在第一象限内的图像上的一点，过点P作于点Q，连接PC，

①求线段PQ的最大值；

②若以P、C、Q为顶点的三角形与相似，求点P的坐标．

Answer 1

【答案】（1）；

（2）①PQ的最大值是；②P的坐标为或

【解析】试题分析：（1）设交点式y=a（x+1）（x-4），再展开可得到-4a=2，解得a=-，即可得到b的值；

（2）①作PN⊥x轴于N，交BC于M，如图，先利用待定系数法求出直线BC的解析式为y=-x+2，设P（t，-t2+t+2），则M（t，-t+2），用t表示出PM=-t2+2t，再证明△PQM∽△BOC，利用相似比得到PQ=-t2+t，然后利用二次函数的性质解决问题；②讨论：当∠PCQ=∠OBC时，△PCQ∽△CBO，PC∥x轴，利用对称性可确定此时P点坐标；当∠CPQ=∠OBC时，△CPQ∽△CBO，则∠CPQ=∠MPQ，所以△PCM为等腰三角形，则PC=PM，利用两点间的距离公式得到t2+（-t2+t+2-2）2=（-t2+2t）2，然后解方程求出t得到此时P点坐标．

试题解析：（1）设抛物线解析式为y=a(x+1)(x4)，

即y=ax23ax4a，

则4a=2,解得a=，

则b=-3a=；

（2）(2)①作PN⊥x轴于N，交BC于M，如图，

BC=，

当x=0时，y=-x2+x+2=2，则C(0，2)，

设直线BC的解析式为y=mx+n，

把C(0，2)，B(4，0)得，解得，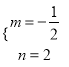

∴直线BC的解析式为y=x+2，

设P(t， t2+t+2)，则M(t， t+2)，

∴PM=t2+t+2(t+2)= t2+2t，

∵∠NBM=∠NPQ，

∴△PQM∽△BOC，

∴，即PQ=，

∴PQ=t2+t= (t2)2+，

∴当t=2时，线段PQ的最大值为；

②当∠PCQ=∠OBC时,△PCQ∽△CBO，

此时PC∥OB,点P和点C关于直线x=对称，

∴此时P点坐标为(3，2)；

当∠CPQ=∠OBC时，△CPQ∽△CBO，

∵∠OBC=∠NPQ，

∴∠CPQ=∠MPQ，

而PQ⊥CM，

∴△PCM为等腰三角形，

∴PC=PM，

∴t2+(t2+t+22)2=(t2+2t)2，

解得t=，

此时P点坐标为(， )，

综上所述,满足条件的P点坐标为(3，2)或(， ).