
【题目】如图是一块△ABC余料,已知AB=20cm,BC=7cm,AC=15cm,现将余料裁剪成一个圆形材料,则该圆的最大面积是_____.
【答案】4πcm2.
【解析】
当该圆为三角形内切圆时面积最大,设内切圆半径为r,则该三角形面积可表示为:![]() r(AB+AC+BC)=21r,过点A作AD⊥BC交BC的延长线于点D,利用勾股定理可求出AD,易得三角形ABC的面积,求出r即可求得圆的面积.
r(AB+AC+BC)=21r,过点A作AD⊥BC交BC的延长线于点D,利用勾股定理可求出AD,易得三角形ABC的面积,求出r即可求得圆的面积.
如图1所示,设三角形内切圆半径为r,
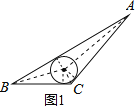
则S△ABC=![]() r(AB+BC+AC)=
r(AB+BC+AC)=![]() r×42=21r,
r×42=21r,
过点A作AD⊥BC交BC的延长线于点D,如图2,
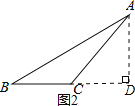
设CD=x,
在Rt△ABD中,由勾股定理得:AD2=AB2﹣BD2=400﹣(7+x)2,
在Rt△ACD中,AD2=AC2﹣x2=225﹣x2,
∴400﹣(7+x)2=225﹣x2,
解得:x=9,
∴AD=12,
∴S△ABC=![]() BC×AD=
BC×AD=![]() ×7×12=42,
×7×12=42,
∴21r=42,
∴r=2,
该圆的最大面积为:S=πr2=4π(cm2),
故答案为:4πcm2.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E,延长CA交⊙O于点F.

(1)求证:DE是⊙O切线;
(2)若AB=10cm,DE+EA=6cm,求AF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=105°,∠DBC=75°.

(1)求证:BD=CD;
(2)若圆O的半径为3,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一批单价为16元的日用品.若按每件23元的价格销售,每月能卖出270件;若按每件28元的价格销售,每月能卖出120件;若规定售价不得低于23元,假定每月销售件数y(件)与价格x(元/件)之间满足一次函数.
(1)试求y与x之间的函数关系式.
(2)在商品不积压且不考虑其他因素的条件下,销售价格定为多少时,才能使每月的毛利润w最大?每月的最大毛利润为多少?
(3)若要使某月的毛利润为1800元,售价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
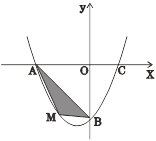
【题目】在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为![]() ,△AMB的面积为S.求S关于
,△AMB的面积为S.求S关于![]() 的函数关系式,并求出S的最大值.
的函数关系式,并求出S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
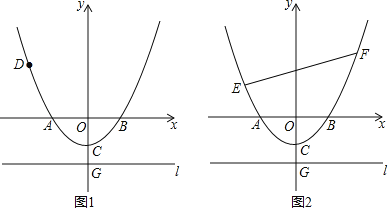
【题目】已知如图1,在以O为原点的平面直角坐标系中,抛物线y=![]() x2+bx+c与x轴交于A,B两点,与y轴交于点C(0,﹣1),连接AC,AO=2CO,直线l过点G(0,t)且平行于x轴,t<﹣1.
x2+bx+c与x轴交于A,B两点,与y轴交于点C(0,﹣1),连接AC,AO=2CO,直线l过点G(0,t)且平行于x轴,t<﹣1.
(1)求抛物线对应的二次函数的解析式;
(2)若D(﹣4,m)为抛物线y=![]() x2+bx+c上一定点,点D到直线l的距离记为d,当d=DO时,求t的值.
x2+bx+c上一定点,点D到直线l的距离记为d,当d=DO时,求t的值.
(3)如图2,若E(﹣4,m)为上述抛物线上一点,在抛物线上是否存在点F,使得△BEF是直角三角形,若存在求出点F的坐标,若不存在说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com