
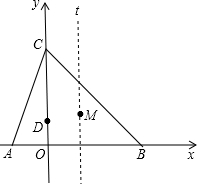
 ��ͼ��ƽ��ֱ�������У�A��-1��0������CΪy����������һ�㣬��AC=
��ͼ��ƽ��ֱ�������У�A��-1��0������CΪy����������һ�㣬��AC=| 10 |
| 2 |
| 10 |
| 10 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 8 |
| AC2-OA2 |
(
|
| BC2-OC2 |
(3
|
| 10 |
| 6 |
| 6 |
| 6 |
| 10 |
| 6 |
| 6 |

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 8 |
| 3 |
| 2 |
| 9 |
| 8 |


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
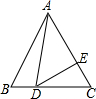 ��ͼ��DΪ�ȱߡ�ABC��BC��һ�㣬��ADE=60�㣬��AC��E����BD=2��CD=3����CE=
��ͼ��DΪ�ȱߡ�ABC��BC��һ�㣬��ADE=60�㣬��AC��E����BD=2��CD=3����CE=�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����OΪԲ�ģ�OA��Ϊ�뾶������OM��ON��A��B���㣬�ٷֱ���ΪA��BΪԲ�ģ���OA��Ϊ�뾶�������������ڵ�C���ֱ�����AC��BC�����ı���OACBһ���ǣ�������
��ͼ����OΪԲ�ģ�OA��Ϊ�뾶������OM��ON��A��B���㣬�ٷֱ���ΪA��BΪԲ�ģ���OA��Ϊ�뾶�������������ڵ�C���ֱ�����AC��BC�����ı���OACBһ���ǣ�������| A������ | B������ | C������ | D�������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
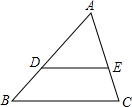 ��ͼ����ABC�У�D��E�ֱ�Ϊ��AB��AC�ϵĵ㣬��DE��BC�������жϴ�����ǣ�������
��ͼ����ABC�У�D��E�ֱ�Ϊ��AB��AC�ϵĵ㣬��DE��BC�������жϴ�����ǣ�������A��
| ||||
B��
| ||||
C��
| ||||
D��
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ��ֱ��AB��ֱ��CD���ڵ�O��OE��AB��OFƽ�֡�AOC������BOD=70�㣮���EOF�Ķ���Ϊ��������
��ͼ��ֱ��AB��ֱ��CD���ڵ�O��OE��AB��OFƽ�֡�AOC������BOD=70�㣮���EOF�Ķ���Ϊ��������| A��115�� | B��125�� |
| C��135�� | D��145�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
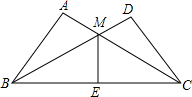 ��ͼ����ABC=��DCB��AB=DC��MEƽ�֡�BMC��BC�ڵ�E��������˵����ȷ���У�������
��ͼ����ABC=��DCB��AB=DC��MEƽ�֡�BMC��BC�ڵ�E��������˵����ȷ���У�������| A��1�� | B��2�� | C��3�� | D��4�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com