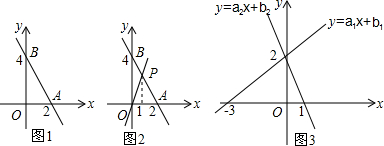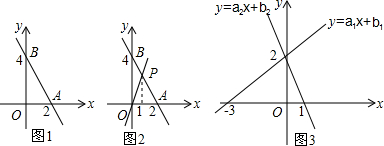3.已知,一次函数y=kx+b(k,b为常数,且k≠0)的图象如图1表示.
(1)方程kx+b=0解为x=2,不等式kx+b<4的解集为x>0.
(2)正比例函数y=mx(m为常数,且m≠0)与一次函数y=kx+b相交于点P(图2),则不等式组$\left\{\begin{array}{l}{mx>0}\\{kx+b>0}\end{array}\right.$的解集为0<x<2.
(3)在(2)的条件下,比较mx与kx+b的大小(直接写出结果);
(4)已知y=a
1x+b
1和y=a
2x+b
2的图象如图3所示,根据图象填空:$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}>0}\\{{a}_{2}x+{b}_{2}>0}\end{array}\right.$的解集是-3<x<1;$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}<0}\\{{a}_{2}x+{b}_{2}>0}\end{array}\right.$的解集是x<-3;$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}>0}\\{{a}_{2}x+{b}_{2}<0}\end{array}\right.$的解集是x>1.